toc

여러 입자의 운동

뉴턴의 프린키피아에서 태양, 지구 그리고 달의 세 천체에 대한 궤도를 그리는 문제로 시작한 삼체 문제(3-body problem)는 이후 앙리 푸앵카레에 의해 일반해가 불가능하다는 것을 증명할 때까지 많은 사람들이 빠져들었던 난제 중 하나였습니다.

여기서는 삼체문제를 확장하여 중력을 주고받는 N개의 입자가 어떤 궤도를 그리는지 알아내기 위해 벌렛(verlet) 방법을 사용합니다.

다체문제

다체 문제

N개의 입자가 중력을 주고받는 상황에서 각 입자가 그리는 궤적을 추적합니다. 벌렛 방법으로 기술하는 각 입자의 운동방정식은 이렇게 쓰입니다.

\[\begin{align} x(t_{i+1}) &= x(t_i) + v(t_i)h + \frac{1}{2} a(t_i)h^2 \\ v(t_{i+1}) &= v(t) + \frac{a(t_{i+1}) + a(t_i)}{2} h \end{align} \\ h = t_{i+1} - t_i\]

벌렛 방법은 아래 과정을 거칩니다.

  1. $ t_0 = 0 $일 때의 초기값 $ x(0) $과 $ v(0) $, 시간 간격 $ h $를 설정합니다.
  2. $ t_1 = t_0 + h $ 일 때의 식 (1)을 풀어 $x_1$을 얻습니다.
  3. 새로운 위치 $x_1$으로부터 $ a(t_1) $을 구합니다.
  4. 앞서 구한 $ a(t_1) $를 이용해 식(2)를 풀어 저장합니다.
  5. $ t_i $의 $ i $를 증가시키면서 원하는 만큼 2~4를 반복합니다.

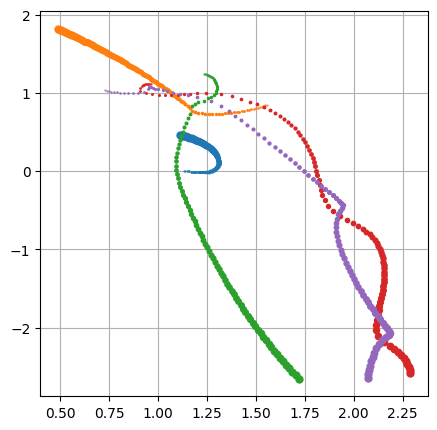
그림은 5개의 입자가 무작위로 배치된 뒤, 무작위의 속도를 가지고 운동하는 궤적을 그린 것입니다.

위치와 속도의 점화식

1
2
3
4
5

def verlet_x(x, v, a):
    """위치 점화식"""
    dx = v * h + 0.5 * a * h ** 2
    return x + dx


1
2
3
4

def verlet_v(v, a):
    """속도 점화식"""
    dv = a * h
    return v + dv

두 함수는 각각 벌렛 절차에 사용하는 $ x(t_{i+1}) $과 $ v(t_{i+1}) $입니다.

주고받는 중력으로부터 가속 계산

1
2
3
4
5
6
7

def acceleration(xy1, xy2, m2):
    """중력을 계산하고 가속도로 출력"""
    r_sq = (xy2[0] - xy1[0]) ** 2 + (xy2[1] - xy1[1]) ** 2
    theta = np.arctan2(xy2[1] - xy1[1], xy2[0] - xy1[0])
    force = m2 / r_sq
    return np.array([force * np.cos(theta), force * np.sin(theta)])

이 함수는 두 입자 사이의 힘과 가속도를 계산합니다. 영향을 받는 입자의 위치 xy1과 영향을 주는 입자의 위치 xy2는 np.array([x, y])형태의 벡터입니다.

입자 1과 입자 n사이의 중력으로 인한 가속는 다음과 같고,

\[a_n(\vec {r}_1, \vec {r}_n, t_{i+1}) = - \frac {m_n (\vec {r}_{1} - \vec {r}_{n}) } {|\vec {r}_{1} - \vec {r}_{n}|^3}\]

이 식이 acceleration()함수와 같은역할을 합니다. 벌렛 모사에 필요한 입자 1에 작용하는 총 가속도는 이렇게 쓸 수 있습니다.

\[a(\vec {r}_1, t_{i+1}) = \sum_n a_n(\vec {r}_1, \vec {r}_n, t_{i+1})\]

벌렛으로 궤도 구하기

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

def particle_motion(time, pos=[], vel=[], mass=[]):
    """벌렛 방법으로 입자의 궤도를 작성"""

    # 위치와 속도 배열 초기화
    pos_arr, vel_arr = [], []
    for _pos, _vel in zip(pos, vel):
        vel_arr.append(np.zeros([time.shape[0], 2]))
        pos_arr.append(np.zeros([time.shape[0], 2]))
        pos_arr[-1][0, :] = _pos
        vel_arr[-1][0, :] = _vel

    # 운동 배열 채우기
    # idx는 t_n의 n을 의미
    for idx in range(1, time.shape[0]):
        # num: 입자 번호, pos: 입자 위치, vel: 입자 속도
        for num, pos, vel in zip(range(len(pos_arr)), pos_arr, vel_arr):

            # acc0: 움직이기 전 가속도
            acc0 = np.zeros(2)
            for pidx in [i for i in range(len(pos_arr)) if i != num]:
                m2 = mass[pidx]
                xy1 = pos[idx - 1]
                xy2 = pos_arr[pidx][idx - 1]
                acc0 += acceleration(xy1, xy2, m2)
            pos[idx, :] = verlet_x(pos[idx - 1], vel[idx - 1], acc0)
            # acc1: 움직인 후의 가속도
            acc1 = np.zeros(2)
            for pidx in [i for i in range(len(pos_arr)) if i != num]:
                m2 = mass[pidx]
                xy1 = pos[idx]
                xy2 = pos_arr[pidx][idx]
                acc1 += acceleration(xy1, xy2, m2)
            vel[idx, :] = verlet_v(vel[idx - 1], (acc0 + acc1) / 2)
    return pos_arr

particle_motion 함수는 벌렛 모사를 실행하는 부분입니다. 함수는 아래 과정을 재현하고 있습니다.

\[\begin{align} x(t_{i+1}) &= x(t_i) + v(t_i)h + \frac{1}{2} a(t_i)h^2 \\ v(t_{i+1}) &= v(t) + \frac{a(t_{i+1}) + a(t_i)}{2} h \end{align} \\ h = t_{i+1} - t_i\]
  1. $ t_0 = 0 $일 때의 초기값 $ x(0) $과 $ v(0) $, 시간 간격 $ h $를 설정합니다.
  2. $ t_1 = t_0 + h $ 일 때의 식 (1)을 풀어 $x_1$을 얻습니다.
  3. 새로운 위치 $x_1$으로부터 $ a(t_1) $을 구합니다.
  4. 앞서 구한 $ a(t_1) $를 이용해 식(2)를 풀어 저장합니다.
  5. $ t_i $의 $ i $를 증가시키면서 원하는 만큼 2~4를 반복합니다.

과제: 지구, 달, 태양의 궤적 모사하기

지구와 태양, 달이 있을 때 한 순간의 위치와 속도를 대입하고 각각의 질량을 초기화변수에 두어 위의 벌렛 알고리즘을 실행합니다. 단, 위의 acceleration()의 force변수에는 중력 상수를 적용하지 않았으므로 이를 수정한 뒤 시행해야 합니다.