물리학을 위한 파이썬
파이썬3를 이용한 전산물리학
물리학을 위한 파이썬
- 버전: 1.1.0 → 1.2.0 (진행중)
Python3를 이용하여 전산물리학의 문제와 해결 방법을 다루는 교재입니다. 교재는 윈도우즈 환경에서 Python 3.9를 기준으로 작성하였습니다.
저작물의 라이선스에 대한 안내
별도 표기가 없는 소스코드는 MIT 라이선스를 따릅니다. 이 교재의 글과 그림은 별도 표기가 없는 경우 크리에이트 커먼즈 저작자표시-비영리-동일조건변경허락(CC BY-NC-SA)를 따릅니다.
저작물 이용에 대한 문의는 아래 연락처를 이용해 주시기 바랍니다.
- 충남대학교 물리학과 교수 강창종(cjkang87@cnu.ac.kr)
- 충남대학교 교육학과 석사과정 진승완(soma0sd@gmail.com)
차례
사전 준비
파이썬 설치하기
여기서는 본격적으로 전산물리학 과정을 시작하기에 앞서 파이썬(Python)을 사용하는 다양한 방법을 소개합니다. 교재의 예제는 파이썬 3.9를 기준으로 작성되었으며 적어도 3.6 이상의 파이썬 배포판을 사용해야 예제와 동일한 결과를 얻을 수 있습니다.
직접 설치를 수행하기 전에 파이썬을 사용하는 다양한 방법이 있으니 개발환경 구성을 미리 계획하고 사용합니다. 파이썬이나 배포판을 2개 이상 설치하는 경우 별도의 지식이 없으면 해석기의 충돌이 생겨 원하는 소스코드로 원하는 결과를 얻을 수 없게 됩니다.
교재는 윈도우 OS에서 파이썬3.9 앱을 설치하고 VSCode로 편집 및 실행하는 환경을 우선 가정하고 있습니다.
- 윈도우 운영체제
- (추천) 아나콘다 배포판을 사용하고 스파이더(Spyder)로 실습
- (추천: 교재의 기준) 윈도우 스토어의 파이썬 앱을 사용하고 VSCode로 실습
- 파이참을 사용하여 실습
- 리눅스 운영체제
- 파이썬 기본판을 사용하고 VSCode로 실습
- 아나콘다 배포판을 사용하고 스파이더(Spyder)로 실습
- 웹브라우저 기반: 개발용 컴퓨터를 사용하기 어렵다면 이런 방법도 있습니다
- (추천) 구글 코렙
- (부분 유료) 구름 IDE
- (현재 클로즈 베타) 깃허브 코드스페이스
윈도우에서 파이썬 설치
파이썬 재단 홈페이지에서 설치 클라이언트를 다운로드 받아 설치하거나 마이크로소프트 스토어에서 파이썬 앱을 설치하는 방법이 있습니다.
리눅스 (우분투 기준)에서 파이썬 설치
1
2
apt update
apt install python3 python3-pip
우분투(Ubuntu) 등 리눅스에 설치하는 경우에는 제공하는 Python3의 버전이 다르니 설치 후 python3 --version을 확인해야 합니다.
아나콘다 설치
아나콘다(Anaconda)는 과학, 통계를 위한 파이썬 패키지가 포함되어 있는 배포판1 입니다. 또한, 완전히 컴파일된 패키지들을 아나콘다 클라우드에서 관리하고 있어서 설치과정에서 복잡한 작업들이 필요한 패키지도 손쉽게 설치할 수 있습니다.
아나콘다 오픈소스(개인)판 다운로드 페이지에 방문하여 설치파일을 내려받아서 설치할 수 있습니다. 아나콘다에는 처음 실행 시간이 조금 오래 걸리지만 강력한 디버깅 도구와 보기 편한 변수 관리 기능들이 포함되어 있는 스파이더(Spyder) 편집기가 포함되어 있습니다.
1: 여러 도구와 패키지 꾸러미를 한데 모은 것으로 파이썬도 여기에 포함됩니다. 아나콘다를 사용하기로 했다면 기존 파이썬을 삭제하는 것이 좋습니다.
VSCode 설치
비주얼 스큐디오 코드 (Visual Studio Code; VSCode) 다양한 언어를 지원하는 소스코드 편집기입니다. 홈페이지에서 설치파일을 내려받아 설치한 후 필요한 확장을 추가로 설치하여 개발환경을 구성합니다. 파이썬과 함께 설치되는 것이 아니니까 아나콘다나 파이썬을 따로 설치해야 합니다.
Python 확장은 가장 기본적인 파이썬 지원도구이며 편리한 개발을 돕는 강력한 도구를 탑재하고 있습니다.
구글 코랩 사용
Google Colaboratory은 구글이 제공하는 램, 메모리, GPU/TPU를 활용할 수 있는 주피터 노트북(Jupyter Notebook) 인터페이스입니다. 구글 계정이 있다면 누구나 손쉽게 활용할 수 있습니다.
실습용 깃허브 저장소 이용하기
깃허브(Github)는 소스코드의 버전관리를 위한 공개/비공개 저장소를 제공합니다. 교재는 깃허브 서비스를 이용하여 예제 코드 및 과제를 위한 저장소를 별도로 운영하고 있습니다.
Git 설치
윈도우:
버전 제어 시스템을 위한 소프트웨어인 깃(Git)을 내려받아 설치합니다. 깃을 설치한 후에 소스트리(Sourcetree)등 전문적인 버전관리 프로그램을 사용하지 않는다면 마이크로소프트의 윈도우 터미널(Windows Terminal) 앱을 사용하는 것이 여러모로 편리합니다.
리눅스(우분투):
1
2
sudo apt update
sudo apt install git
실습 저장소 복제
편한 곳에 새로운 디렉토리를 만들어 저장소를 복제합니다. 충돌 없이 저장소를 복제하려면 파일이 들어있지 않은 폴더를 하나 생성하는 것이 좋습니다. 윈도우 사용자의 경우 c:/Github, 리눅스 사용자의 경우 mkdir ~/Github와 같은 방식으로 디렉토리를 만듭니다.
새로 만든 디렉토리로 이동하여 터미널을 실행합니다. 윈도우 OS에서는 파일탐색기로 연 폴더의 바닥에서 Shifht + 마우스 오른쪽 버튼을 눌러 “여기에 파워쉘 창 열기” 메뉴를 선택하거나 앞서 윈도우 터미널 앱을 설치했다면 마우스 오른쪽 버튼으로 “Open in Windows Terminal”를 선택할 수 있습니다. 리눅스의 경우에는 터미널에서 cd ~/Github등으로 이동합니다.
1
git clone https://github.com/CNU-Computer-Physics/Example-and-Practice
으로 간단하게 터미널을 복제할 수 있습니다.
내 저장소로 포크
저장소를 포크(Fork)하여 내 소유로 만들면 개인 성과로 관리하기도 편하고 예제를 변경하여 새로운 소스코드로 만들어 관힐할 수 있습니다. 예제 깃허브 홈페이지에 방문하여 오른쪽의 “Fork” 버튼을 클릭하면 내 소유의 예제 저장소를 만들 수 있습니다. 포크한 저장소는 https://github.com/{내 깃허브 ID}/Example-and-Practice에 위치하며 개인 저장소에 있기엔 이름이 애매하다 싶으면 저장소 페이지 상단에서 “Settings” 메뉴를 눌러 저장소의 이름을 바꿀 수 있습니다. 저장소의 이름을 바꾸면 URL도 바뀌니 복제할 때 주의해야 합니다.
저장소를 포크했다면 내 컴퓨터의 저장소용 디렉토리에서
1
git clone https://github.com/{내 깃허브 ID}/{포크한 저장소의 이름}
과 같은 방식으로 복제할 수 있습니다.
포크한 저장소 업데이트
예제 저장소가 업데이트 되었을 때 이것을 내 저장소에 적용하고 싶다면 다음 절차를 따릅니다.
- 복제한 저장소의 디렉토리(ex.
Example-and-Practice/)안에서 터미널 열기 - 원본 리모트 추가:
git remote add upstream https://github.com/CNU-Computer-Physics/Example-and-Practice - 원본으로부터 패치:
git fetch upstream - 원본과 내 저장소를 병합:
git merge upstream/main - 내 저장소로 밀어넣기:
git push
파이썬 기본 문법 학습
파이썬 기초 학습 커리큘럼을 제작중입니다. 교재가 준비 될 때까지 프로그래밍과 파이썬 기초문법은 아래의 웹 교재를 참고하시기 바랍니다.
Python 3.9.6 문서
Python 3.9.6 문서의 자습서는 파이썬 재단이 추천하는 파이썬 학습 코스입니다.
점프 투 파이썬
점프 투 파이썬은 한국에서 가장 유명한 파이썬 입문서 중 하나입니다.
그래프 그래기
그래프 패키지 설치하기
matplotlib은 파이썬을 위한 시각화 도구입니다. 각종 그래프와 그림, 다이얼로그등을 다루는 것을 목적으로 합니다. 추가로 설치하는 NumPy와 SciPy는 수치해석, 통계, 과학 등을 위한 각종 함수와 데이터형을 제공합니다.
여기서는 파이썬으로 그래프를 그리는데 필요한 패키지를 설치하고 패키지가 제대로 설치되었는지 확인하도록 합니다.
앞으로의 실습에 필요한 matplotlib과 numpy, scipy를 설치합니다. 구글 코랩(Google Colab)이나 아나콘다(Anaconda)를 사용하는 경우, 이 패키지들은 미리 설치되어 있으니 굳이 설치할 필요가 없습니다.
PIP 설치 및 업그레이드
1
python3 -m pip install --upgrade matplotlib numpy scipy
아나콘다(Anaconda) 설치 및 업그레이드: 보통은 기본으로 설치되어 있습니다.
1
conda install --upgrade matplotlib numpy scipy
리눅스 설치
1
2
sudo apt update && sudo apt upgrade
sudo apt install python3-matplotlib python3-numpy python3-scipy
matplotlib.pyplot
matplotlib는 너무 복잡한 모듈과 설정을 가지고 있어서 수업에는 쉽고 단순한 인터페이스를 제공하는 pyplot모듈을 이용합니다.
1
2
3
4
5
6
import matplotlib.pyplot as plt
x = [1, 2, 3]
y = [3, 1, 4]
plt.plot(x, y)
plt.show()
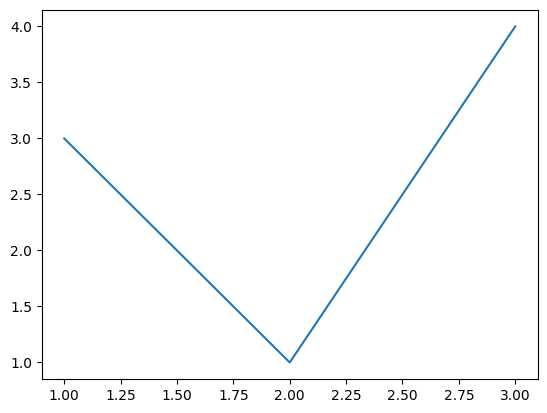
위 예제를 실행하면 새로운 창에 그림과 같은 그래프를 포시합니다. 아나콘다(Anaconda)의 스파이더(Spyder) 편집기를 사용하거나 구글 코랩(colab) 등 주피터 노트북(Jupyter notebook)기반의 편집기에서 실행하는 경우 결과 표시 창에 그래프를 출력합니다.
matplotlib의 예제(Example)과 튜토리얼(Tutorials) 문서들을 통해 다양한 그림을 작성하는 방법을 배울 수 있습니다.
NumPy, SciPy
NumPy는 수치해석 및 행렬연산을 위한 다양한 도구와 새로운 자료형 등을 제공합니다. NumPy 설명서를 통해서 상세한 기능들을 살펴볼 수 있습니다. SciPy는 과학을 위한 특수함수 및 통계 등을 제공합니다. SciPy 설명서를 통해서 상세한 설명을 살펴볼 수 있습니다.
함수의 그래프
예제: 사용자가 지정한 함수 그리기
$ \sin(x) $ 함수를 그래프로 그립니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
"""사용자가 지정한 함수 그리기
sin(x) 함수를 지정한 범위 [0, 3Pi]의 그래프로 그려서 출력하기
"""
import numpy as np
import matplotlib.pyplot as plt
def func(x):
return np.sin(x)
if __name__ == "__main__":
x = np.linspace(0, np.pi * 3)
plt.plot(x, func(x))
plt.grid(True)
plt.show()
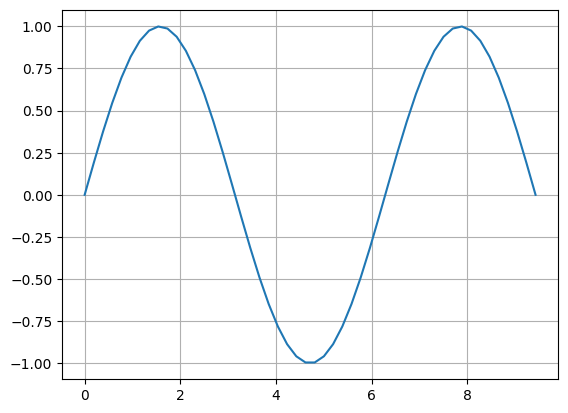
np.linspace(0, 3)은 0부터 3사이 숫자를 일정 간격으로 50개(기본값) 만들어 numpy의 array 자료형으로 출력합니다. 출력 결과는 [0.00, 0.06, 0.12,..] 형태입니다.
np.linspace(xmin, xmax, ndata) 는 xmin 부터 xmax 사이 숫자를 일정 간격으로 ndata 개수만큼 생성하여 numpy 의 array 자료형으로 출력합니다.
plt.grid(True)를 사용하여 그래프에 격자 보조선을 넣을 수 있습니다.
과제: 여러 종류의 함수를 그리기
다음 함수를 정해진 범위에 따라 그립니다.
- $ \cos(x) $, x는 [-$ \pi $, +2$ \pi $]
- numpy 활용:
np.cos(x)
- numpy 활용:
- $ 3x + 2 $, x는 [0, 5]
3 * x + 2
- $ \ln(x) $, x는 [0, 10]
- numpy 활용:
np.log(x)
- numpy 활용:
- $ e^{x} $, x는 [-5, 5]
- numpy 활용:
np.exp(x)
- numpy 활용:
데이터 파일을 그래프로
데이터파일 02_plotting/input.csv은 아래와 같이 공백으로 구분한 두 실수로 작성되어 있습니다.
0.0202184 1.0819082
0.07103606 0.87027612
0.0871293 1.14386208
0.11827443 0.70322051
... ...
이 파일의 첫 번째 열은 x값 두 번째 값은 y값이라고 약속했을 때 이 데이터를 그래프로 그리려고 합니다.
- 예제 파일:
02_plotting/02_data_plot.py
프로그래밍
파일 내용 읽어들이기
1
2
3
4
5
6
7
8
9
x = []
y = []
with open("input.csv", "r") as f:
for line in f.readlines():
items = line.split(" ")
x.append(float(items[0]))
y.append(float(items[1]))
with open({파일}, {모드}) as {더미}:는 파일을 열어서 사용하기 위한 문법입니다. {파일}을 {모드}로 읽어서 {더미}에 변수로 저장합니다. 즉, 위의 예시에서는 input.csv를 읽기(r)모드로 변수 f에 저장합니다.
f.readlines()는 파일 내용을 한줄씩 문자열로 읽어 리스트형 변수로 만듭니다. 각 문자열(line)을 공백을 기준으로 분할하고 각각을 x변수와 y변수에 추가(append())합니다. 문자열을 수치로 받아들일 수 있도록 float()를 사용하여 변수의 자료형을 변경합니다.
데이터를 그래프로 그리기
1
2
3
4
5
6
7
8
9
10
import matplotlib.pyplot as plt
if __name__ == "__main__":
plt.scatter(x, y)
plt.xlim(0, 5)
plt.ylim(0, 30)
plt.grid(True)
# plt.savefig("data_plot_1.png", bbox_inches="tight")
plt.show()
plt.scatter(x, y)는 분산형 그래프를 그리는 함수입니다. plt.xlim(min, max)과 plt.ylim(min, max)은 각 축의 최소값과 최대값을 지정합니다.
주석으로 처리되어 있는 plt.savefig()는 결과를 그림 파일로 저장하고록 하는 명령입니다. 10번 줄을 주석 처리하고 9번의 주석을 해제하면 주어진 이름의 그림 파일로 그래프를 출력합니다. 예제 그대로 실행하면 plt.show() 명령에 따라 창에 그래프를 표시합니다.
결과
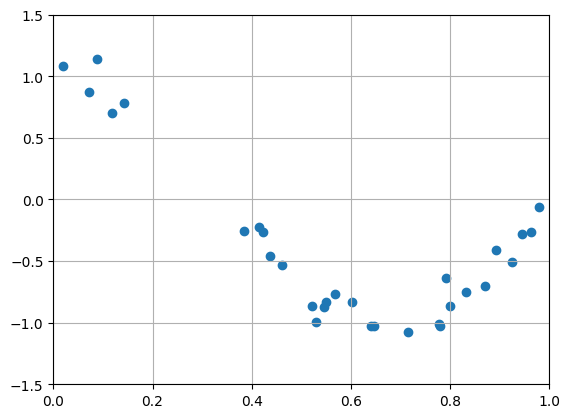
plt.scatter(x, y)로 표시한 그래프는 앞의 함수를 그래프로 그렸을 때 사용한 plt.plot(x, y)와는 다르게 데이터를 점으로 표시합니다.
히스토그램 작성
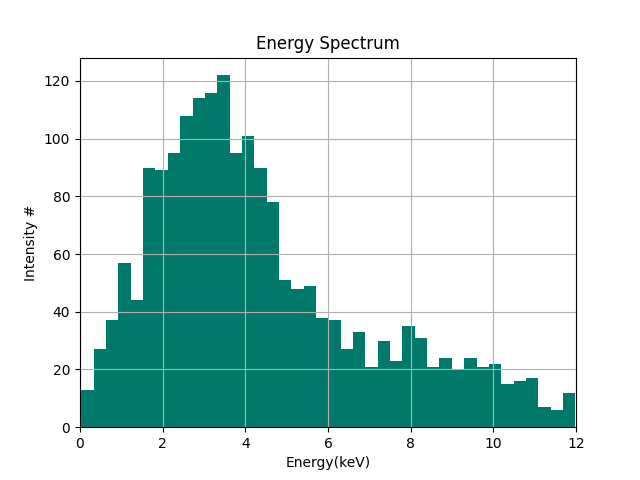
히스토그램은 데이터의 도수분포를 그림으로 나타낸 것입니다. 여기서 소개할 matplotlib의 hist함수는 영역을 구간으로 나눈 계급을에 따라 데이터를 분류하고 누적량을 그래프와 데이터로 출력합니다.
1차원 히스토그램
- 예제 파일:
02_plotting/03A_histogram.py - 데이터 파일:
02_plotting/hist.csv
1차원 데이터
데이터파일은 1904줄의 1차원 배열이며 각 줄마다 측정한 수치가 들어있습니다.
8.119651934101998592e+00
1.008247783750474191e+01
4.341979401586036680e+00
7.326366608122442337e+00
1.064307895804619442e+01
...
1차원 히스토그램 그리기
히스토그램을 사용하여 각 데이터의 도수 분포를 집계하고 결과를 그래프로 표시합니다.
1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import matplotlib.pyplot as plt
data = np.loadtxt("hist.csv")
n, bins, p = plt.hist(data, bins=40, color="#00796B")
plt.title("Energy Spectrum")
plt.xlabel("Energy(keV)")
plt.ylabel("Intensity #")
plt.xlim(0, 12)
plt.grid()
plt.show()
데이터를 np.loadtxt()로 읽은 후 plt.hist()에 전달하여 출력합니다. 여기서 bins 속성은 몇 개의 계급으로 표시할지를 정합니다. 잘 와닿지 않는다면 이 속성값을 2와 10으로 바꾼 뒤 그래프가 어떻게 나오는지 살펴보도록 합니다.
plt.hist()의 공식 API 문서
2차원 히스토그램
- 예제 파일:
02_plotting/03B_histogram.py - 데이터 파일:
02_plotting/hist2D.csv
2차원 데이터
2치원 데이터는 csv 형식으로 작성되어 있습니다. 쉼표 ,를 기준으로 x와 y로 나뉘어 5000줄로 작성되어 있습니다.
-2.738838974609301147e+00, -6.367595643836828856e+00
1.963398912200970958e+00, 6.984811270124598792e+00
8.283667139098009002e+00, -1.337330966827691192e+01
..., ...
2차원 히스토그램 그리기
1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import matplotlib.pyplot as plt
data = np.loadtxt("hist2D.csv", delimiter=", ")
fig, ax = plt.subplots()
hist = ax.hist2d(data[:, 0], data[:, 1], bins=40, range=([0, 10], [0, 10]))
fig.colorbar(hist[3], ax=ax)
plt.xlabel("Position X")
plt.ylabel("Position Y")
plt.grid()
plt.show()
2차원 히스토그램은 hist2d()를 사용하여 표시할 수 있습니다. 별도로 색상바를 표시하기 위해 hist의 결과값을 사용합니다.
plt.hist2d()의 공식 API 문서
결과
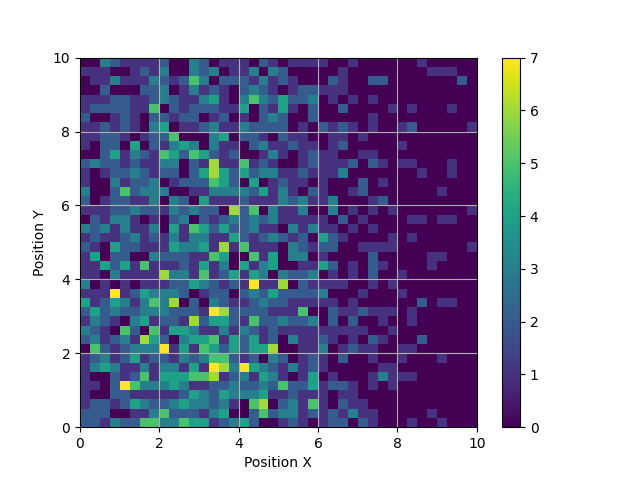
2차원 히스토그램은 2차원 평면에서 높이를 표시하기 어렵기 때문에 색상을 사용해서 한 차원을 더 표시합니다. 히스토그램을 그리는 함수는 결과값으로 계급과 수치를 내놓기 때문에 이후 분석에도 활용할 수 있습니다.
데이터 분석
데이터 피팅
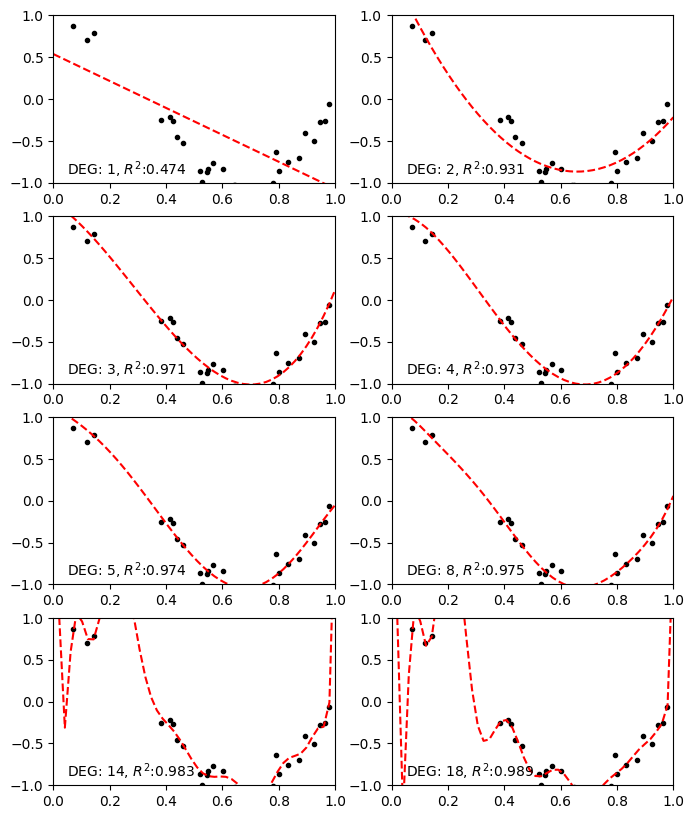
앞서 그린 데이터 그래프를 토대로 다항식 모델을 세워 계수를 알아내려고 합니다.
\[f(x) = \sum _i a_i x^{i}\]위의 다항식 모델에서 $ i $는 모델의 최고차수를 나타내며 $ a_i $는 각 차수에 해당하는 계수를 나타내는 수치입니다. 데이터 다항식 피팅의 목표는 $ A = [a_0, a_1, a_2, ..] $를 얻어내는 것입니다. 찾아낸 $ A $는 이후 데이터 분석 등을 수행할 때 가설과 얼마나 일치하는지 확인하거나 외삽, 내삽을 이용하여 필요한 추정치를 얻고자 할 때 중요한 참고가 됩니다.
여기서는 np.polyfit()을 사용하여 $ A $를 구합니다. 정확히 어떤 방식으로 계수를 구하는지 알고 싶다면 최소제곱법에 대해 조사해봅시다.
아래의 프로그램은 여러 차수에 대해 다항식 피팅을 수행하고 그래프로 표시합니다.
- 데이터 파일:
03_analysis/input.csv - 실습 파일:
03_analysis/01_data_fitting.py
프로그래밍
파일 읽어들이기
input.csv파일의 내용은 아래와 같이 공백으로 구분한 두 실수입니다.
0.0202184 1.0819082
0.07103606 0.87027612
0.0871293 1.14386208
0.11827443 0.70322051
... ...
이 파일을 읽어들여 x, y의 두 실수 리스트를 만들도록 합니다.
1
2
3
4
5
6
7
8
x = []
y = []
with open("input.csv", "r") as f:
for line in f.readlines():
_x, _y = [float(i) for i in line.split(" ")]
x.append(_x)
y.append(_y)
이처럼 데이터 파일의 형식을 명확하게 알고 있는 경우 축약표현을 사용할 수 있습니다. [float(i) for i in line.split(" ")]는 문자열 line을 공백 기준으로 나누고 각각을 float()로 실수형 값으로 변환합니다.
최적화 계수 구하기
1
2
3
4
5
6
7
8
9
degs = [1, 2, 3, 4, 5, 8, 14, 18]
for idx, deg in enumerate(degs):
coef = np.polyfit(x, y, deg)
fit = np.poly1d(coef)
sst = np.sum(np.power(y - np.average(y), 2))
ssr = np.sum(np.power(y - fit(x), 2))
sqr = 1 - (ssr / sst)
print(f"======= DEG: {deg}, R^2:{sqr:.3f} =======")
print(coef)
나열하는 원소(deg)와 몇 번째 원소인지(idx)를 받아오기 위해 enumerate(degs)를 사용합니다.
np.polyfit(x, y, deg)은 데이터의 x값과 y값, 차수가 주어지면 다항식 계수의 행렬을 출력합니다. 계수의 배열은 차수가 낮은 것부터 높은 순으로 정렬되어 있습니다.
계수의 행렬을 간단하게 다항식 함수로 만들어 주는 것이 np.poly1d(coef)입니다. 값이 아닌 함수를 출력합니다.
변수 sqr은 결정계수($ r^2 $)를 담고 있습니다. 추정하는 모델의 함수가 $ g(x) $일 때, $ r^2 $은 아래와 같이 계산합니다.
한 그림에 여러 그래프 표시하기
1
2
3
4
5
6
7
8
9
10
11
12
13
degs = [1, 2, 3, 4, 5, 8, 14, 18]
new_x = np.linspace(0, 1)
plt.figure(figsize=(8, 10))
for idx, deg in enumerate(degs):
# ...적합 계수와 결정계수 계산...
# 서브플롯 명령
ax = plt.subplot(4, 2, idx + 1)
ax.set_xlim(0, 1)
ax.set_ylim(-1, 1)
ax.text(0.05, -0.9, f"DEG: {deg}, $R^2$:{sqr:.3f}", fontsize=10)
ax.plot(x, y, ".k")
ax.plot(new_x, fit(new_x), "--r", label="DEG: {}".format(deg))
plt.savefig("01_data_fitting.png", bbox_inches="tight")
plt.figure()는 그림의 속성을 지시합니다. 사용한 figsize=(8, 10) 속성은 그림의 크기를 지시하며, 가로 8인치, 세로 10인치인 그림을 그릴 것이라는 표시가 됩니다.
4행 2열 그래프 중 idx + 1번째1 그래프를 지시하기 위해 plt.subplot(4, 2, idx + 1)를 사용합니다.
만든 그림을 바로 보는 대신 그림파일로 저장하는 명령인 plt.savefig()를 사용하여 fitting.png로 저장합니다.
1: 원소는 0부터 세지만 그림은 1부터 세기 때문에 원소의 번호인 idx에 1을 더합니다.
함수를 미분하기
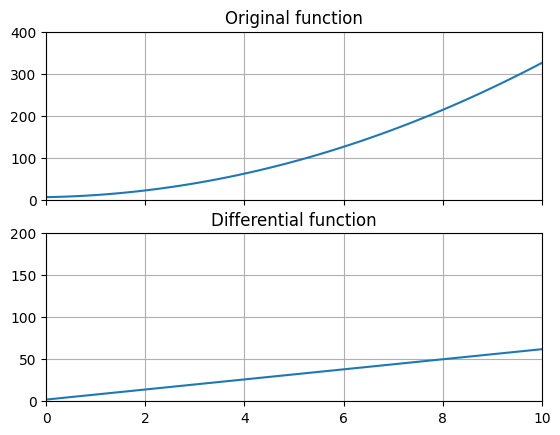
함수$ f(x) $를 미분하는 경우 아래의 과정을 거치게 됩니다.
\[f'(x) = \lim _{\Delta x \to 0} \frac {f(x + \Delta x) - f(x)} { \Delta x }\]그러나 컴퓨터는 무한소 개념을 이해 할 수 없으므로 충분히 작은 값 $ h $를 도입합니다. 수학적으로 엄밀하지 않고 오차가 발생하겠지만 수치를 다룰 때 신경쓰이지 않을 정도로 작은 오차를 낼수 있는 충분히 작은 $ h $를 사용한다면 큰 문제없이 수치해석에 사용할 수 있습니다.
\[f'(x) = \frac {f(x + h) - f(x)} { h }, h \ll 1\]도함수 만들기
원함수
1
2
def f(x):
return np.sin(x)
도함수를 구할 원함수 $ \sin x $입니다.
미분 함수
1
2
3
4
5
6
7
8
def g(func, xmin, xmax, h=0.01):
x = np.arange(xmin, xmax, h)
y = []
y0 = func(xmin)
for _x in x:
y0 += func(_x + h) - func(_x)
y.append(y0)
return x, np.array(y)
원함수 func와 $ x $의 시작값인 xmin, $ x $의 끝값인 xmax, 미분 간격 h을 입력받아 미분한 함수값들을 출력합니다.
식의 파이썬 표현입니다.
그래프 그리기
1
2
3
4
5
x = np.linspace(0, np.pi * 10, 100)
plt.plot(x, f(x), "k--")
plt.plot(*g(f, 0, np.pi * 10, h), "r")
plt.grid(True)
plt.show()
plt.plot()의 세 번째 매개변수인 "k--"는 검정색(k), 점선(--)을 의미하는 약식 속성입니다. plt.grid(True)를 통해 그래프에 보조 격자선을 표시할 수 있습니다.
컴퓨터로 계산한 도함수의 오차
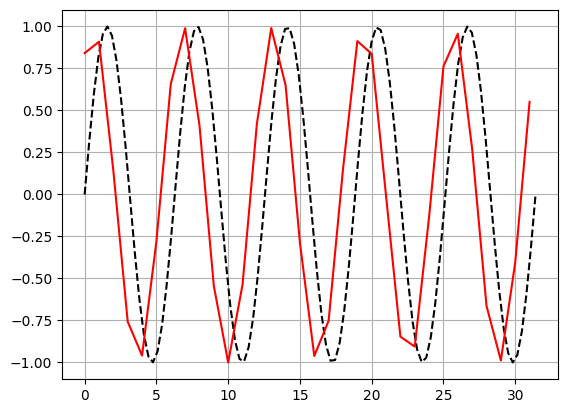
이 프로그램은 도함수를 사용해서 원래 함수와 같은 값을 출력하도록 만든 것입니다.
\[f(x_{i}) = f(x_{i-1}) + h f'(x_{i})\]즉,
\[f(x_{i}) = f(x_{i-1}) + f(x_{i} + h) - f(x_{i})\]이 됩니다.
위의 예제를 실행해 보고 h의 크기에 따라 오차가 어떻게 변하는지 살펴봅시다.
1
2
3
4
5
6
7
8
def g(func, xmin, xmax, h=0.01):
x = np.arange(xmin, xmax, h)
y = []
y0 = func(xmin)
for _x in x:
y0 += func(_x + h) - func(_x)
y.append(y0)
return x, np.array(y)
검증함수 g(func, xmin, xmax, h)는 각각 함수 func, 시작값 xmin, 끝나는 값 xmax, 데이터 간격 h를 입력을 받아 데이터 배열 x와 y를 출력합니다. 함수의 매개변수 표현 중 h=0.01이 있습니다. 이것은 “h값 입력을 생략했다면 h의 값으로 0.01을 사용한다”는 뜻입니다.
정해진 간격 h를 두고 xmin부터 xmax에 이르는 배열을 얻기 위해 np.arange(xmin, xmax, h)를 사용합니다.
1
2
plt.plot(x, f(x), "k--")
plt.plot(*g(f, 0, np.pi * 10, h), "r")
plt.plot의 세 번째 옵션인 "k--"는 검은색(k) 점선(--)으로 표시하라는 의미를 가지고 있습니다. "r"은 빨강(r)색으로 바꾸고 나머지는 기본값으로 표시하라는 의미를 가집니다.
예제는 특수한 매개변수 전달 방식으로 *g(f, 0, np.pi * 10, h)을 사용하고 있습니다. 이것은 풀기(unpack)라는 사용방법이며 묶여있는 상태의 매개변수들을 풀어서 대입할 수 있도록 합니다.
데이터를 미분하기
여기서는 데이터를 미분한 것과 데이터를 피팅한 후 미분한 것을 비교하도록 합니다.
프로그래밍
데이터 읽어들이기
이전 데이터 피팅에서 사용했던 input.csv파일을 그대로 사용합니다. 내용은 아래와 같이 공백으로 구분한 두 실수입니다.
0.0202184 1.0819082
0.07103606 0.87027612
0.0871293 1.14386208
0.11827443 0.70322051
... ...
이 파일을 읽어들여 x, y의 두 실수 리스트를 만들게 됩니다.
1
2
3
4
5
6
7
8
x = []
y = []
with open("input.csv", "r") as f:
for line in f.readlines():
_x, _y = [float(i) for i in line.split(" ")]
x.append(_x)
y.append(_y)
데이터의 미분
함수의 미분과 같은 방식으로 데이터 미분을 수행합니다.
1
2
3
4
5
6
7
def g(x, y):
new_x = []
new_y = []
for idx in range(len(x) - 1):
new_x.append((x[idx] + x[idx + 1]) / 2)
new_y.append((y[idx + 1] - y[idx]) / (x[idx + 1] - x[idx]))
return new_x, new_y
함수는 아래의 수식과 같은 기능을 합니다.
\[y_i = \frac {f(x_{i+1}) - f(x_i)} { x_{i+1} - x_i }\] \[x_i = \frac {x_{i+1} + x_i} {2}\]데이터를 피팅하고 미분
1
2
3
4
# 2차함수로 피팅한 x와 y
fit = np.poly1d(np.polyfit(x, y, 2))
fit_x = np.linspace(0, 1)[:-1]
fit_y = np.diff(fit(fit_x))
np.diff()는 배열의 한 축을 정하고 그 축을 따라 변화량을 계산해서 새로운 배열로 돌려줍니다. 1차원 배열이 들어간 경우 순서상으로 이웃한 두 값 사이의 변화량을 출력하며 배열의 크기는 하나 줄어들게 됩니다.
결과
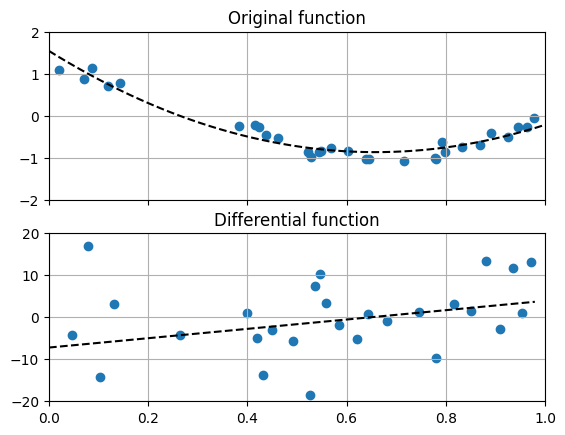
앞서 다뤘던 함수의 도함수를 계산하는 요령으로 데이터의 미분량을 구하는 함수가 g()입니다. 그래프에는 점으로 표현되어 있는 값입니다.
이와는 별도로 데이터 피팅을 우선 수행하여 fit_x와 fit_y로도 계산하여 그래프에 검정색 실선으로 표시하였습니다.
우리가 현상이나 특성의 모델을 세우고 이를 확인하고자 할 때 도움이 되는 방법은 무엇일까요?
함수의 적분
함수를 구간적분하고 적분 값과 적분 구간을 그래프에 표시합니다.
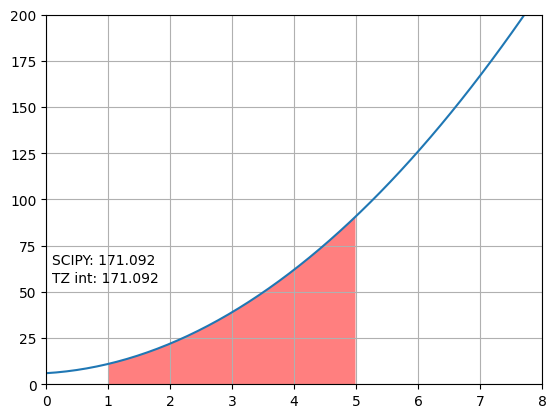
이 프로그램은 사다리꼴 적분을 직접 int_f() 함수로 구현해서 사용하는 방법과 scipy의 integrate.trapezoid함수를 이용하는 방법을 각각 실행하고 결과를 그래프상에 표시합니다.
그림의 SCIPY는 scipy에서 제공하는 적분함수 trapezoid()로 계산한 적분량, TZ int는 직접 만든 int_f()로 계산한 적분량입니다. 적분 영역은 빨간색으로 표시하였습니다.
사다리꼴 적분
1
2
3
4
5
6
def int_f(func, x_min, x_max, h):
output = 0
x = np.arange(x_min, x_max, h)
for idx in range(len(x) - 1):
output += (func(x[idx]) + func(x[idx + 1])) * h / 2
return output
를 함수로 구현한 부분입니다. h는 $ \text {d} x $, func는 $ f(x) $, x_min과 x_max는 적분 구간을 나타냅니다.
채워진 곡선 그리기
1
2
3
4
5
6
7
8
x_inf = np.arange(min_x, max_x, h)
y_inf = f(x_inf)
x_inf = np.concatenate(([x_inf[0]], x_inf, [x_inf[-1]]))
y_inf = np.concatenate(([0], y_inf, [0]))
plt.fill(x_inf, y_inf, "r", alpha=0.5)
plt.grid(True)
plt.show()
plt.fill()은 채워진 곡선을 얻고자 할 때 씁니다. 곡선을 가장 적은 넓이로 닫을 수 있는 도형을 택하기 때문에 종종 원하지 않는 결과가 나오기도 합니다. 이를 해결하기 위해 np.concatenate()을 사용하여 생길 도형을 강제시킵니다.
np.concatenate((a, b, c))는 배열 a, b, c를 순서대로 붙인 배열을 출력합니다.
plt.fill()에서 사용한 "r"과 alpha=0.5는 각각 빨강으로 채우되 투명도는 50%로 할 것을 지시합니다.
데이터의 적분
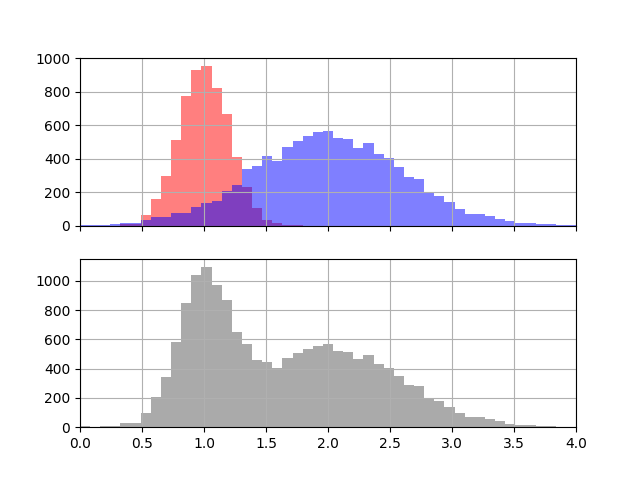
그림은 가상의 반응에 의해 발생한 입자 A(빨강)와 B(파랑)의 에너지 스펙트럼 입니다. 반응이 일어나는 환경에서 일정 시간동안 입사하는 입자의 에너지를 측정하여 히스토그램 형태로 표시하였습니다. 그림 상단은 각 입자의 스펙트럼, 하단은 실제로 얻게 될 스펙트럼입니다.
실제 실험에서 우리는 아래의 데이터만을 얻게 됩니다. 서로 다른 운동 예너지를 가진 두 종류의 입자를 검출했다는 사실 정도만 알 수 있습니다.
여기서 우리는 가상의 반응이 지닌 특성을 알아내기 위해 가상의 반응이 생성하는 입자 A와 입자 B의 비율을 알고 싶습니다.
- 실습 파일:
03_analysis/05_data_integration.py - 데이터 파일:
03_analysis/hist.csv
데이터 형식
주어진 데이터는 아래와 같은 형식을 가지고 있습니다. 데이터를 쉼표로 구분하는 것은 csv형식의 특징입니다. 1열은 에너지 채널의 최소값을 의미하고, 2열은 측정시간동안 채널에 해당하는 입자가 몇 개 측정되었는지를 나타냅니다.
0.0000, 6
0.0816, 4
0.1633, 5
0.2449, 8
0.3265, 26
0.4082, 28
0.4898, 95
0.5714, 209
...
파일을 읽어들여 각각 bins와 count에 넣어둡니다.
1
2
3
4
5
6
bins, count = [], []
with open("hist.csv", "r") as f:
for line in f.readlines():
_b, _c = [float(i) for i in line.split(",")]
bins.append(_b)
count.append(_c)
커브 피팅 함수
scipy.optimize.curve_fit() 함수는 직접 만든 모델의 최적 계수를 찾아줍니다. 이를 이용해서 피팅을 수행하고 계수를 찾아 적분에 필요한 정보를 얻습니다. 판단에 따라 다양한 모델 중 하나를 구현해서 사용할 수 있습니다. 여기서는 일반적으로 사용하는 가우시안(정규분포) 모델을 사용하도록 하겠습니다.
사용할 가우시안의 선형결합입니다.
1
2
3
4
5
6
7
8
9
10
def particle(x, a, b, c):
return a * np.exp(-((x - b) ** 2) / (2 * c ** 2))
def model(x, a_0, a_1, a_2, a_3, a_4, a_5):
p_a = particle(x, a_0, a_1, a_2)
p_b = particle(x, a_3, a_4, a_5)
return p_a + p_b
popt, pcov = curve_fit(model, bins, count, p0=[100, 1, 0.1, 100, 4, 0.1])
p0 옵션은 나중에 선형 결합된 상태로 피팅한 결과를 다시 각 입자의 에너지 스펙트럼으로 변환하는 과정에서 무엇이 입자 A, 입자 B의 결과인지 알기 쉽게 하기 위해 초기 변수를 지정하는 것입니다. 0번과 3번 값은 함수값의 최대치와 관련이 있고, 1번과 4번은 가우시안의 중앙이 어디에 있는지, 2번과 5번은 분산과 관련이 있습니다.
1번과 4번 초기값을 미리 주는 방법으로 어떤 입자의 에너지 스펙트럼인지 알기 쉽도록 만들었습니다.
popt는 최적값의 배열, popv는 공분산 배열입니다. 직접 출력해서 확인해 볼 수 있습니다. 공분산 popv로부터 표준 편차를 계산하려면 np.sqrt(np.diag(pcov))를 사용합니다.
1
2
3
4
5
6
7
xdata = np.linspace(0, 4, 100)
plt.plot(xdata, model(xdata, *popt), "k")
plt.plot(xdata, particle(xdata, *popt[:3]), "r")
plt.plot(xdata, particle(xdata, *popt[3:]), "b")
plt.bar(bins, count, 0.05, color="#AAA")
plt.show()
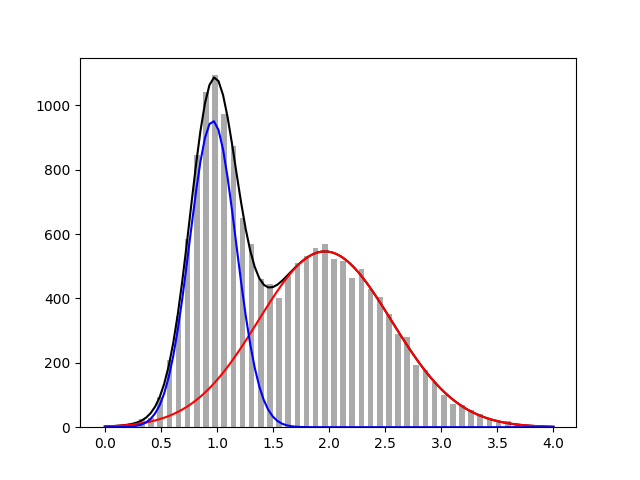
피팅 결과를 눈으로 확인해봅시다. 우리가 세운 모델을 사용하여 두 입자의 스펙트럼을 분리할 수 있는 것을 볼 수 있습니다. 분리한 입자별 에너지 스펙트럼을 통해 다양한 정보를 얻을 수 있습니다.
xdata는 내삽을 적용하여 더욱 정밀한 값을 얻기 위해 np.linspace()함수를 사용했습니다.
적분 연산
앞서 두 입자의 생성비를 계산하기 위해 앞서 구한 모델로부터 두 입자의 함수를 구했습니다. 이제 각각의 에너지 스펙트럼을 적분하여 몇 개의 입자가 생성되었는지 비교하는 작업이 남았습니다.
적분을 통해 입자의 생성비를 계산할 수 있습니다. 여기서는 이전 시간에 검증한 scipy.integrate.trapezoid() 함수를 사용합니다.
1
2
3
4
5
6
7
p_a_value = trapezoid(particle(xdata, *popt[:3]), xdata)
p_b_value = trapezoid(particle(xdata, *popt[3:]), xdata)
print(f"Particle A: {p_a_value:.2f}")
print(f"Particle B: {p_b_value:.2f}")
print(f"Proportion particle data (A/B): {p_a_value/p_b_value:.3f}")
print(f"Proportion particle reference (A/B): {6000/10000:.3f}")
마지막 줄은 예제로 사용했던 데이터를 생성할때 정한 비율입니다.
시뮬레이션
뉴턴 방법
여기서는 뉴턴 방법(Newton method)을 이용해 해를 찾는 방법과 운동하는 물체의 경로를 찾는 방법을 알아봅니다.
뉴턴 방법으로 해 찾기
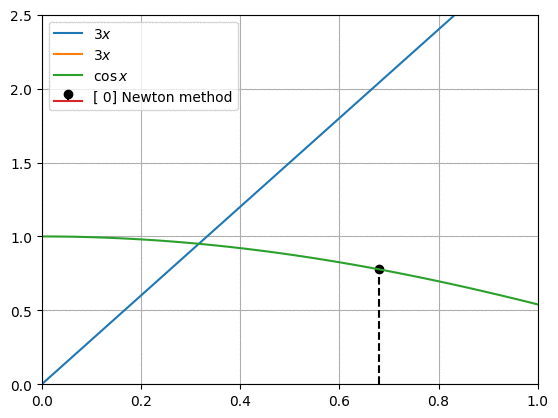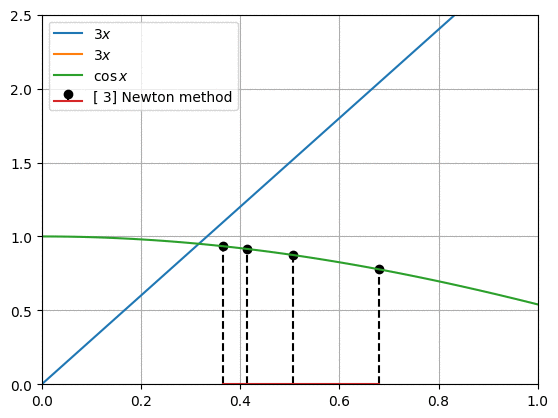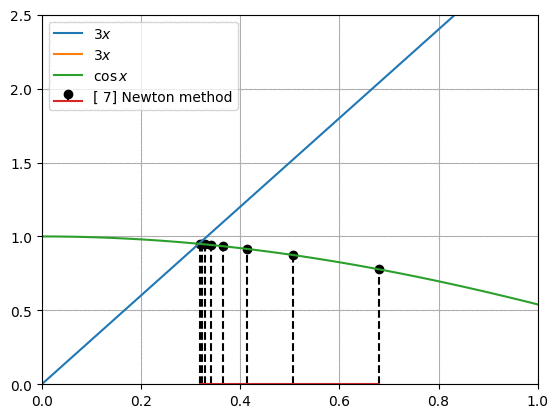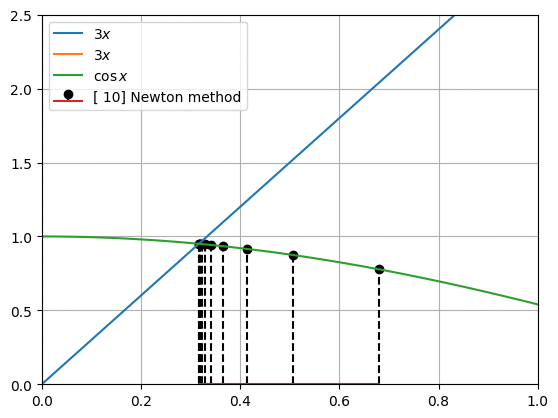
뉴턴 방법(Newton method)은 아래와 같은 점화식을 가집니다.
\[x_n = x_{n-1} - \frac {f(x_{n-1})} {f'(x_{n-1})}\]이 점화식을 반복할수록 극한값을 가지는 $x_n$에 수렴하게 될 것입니다. 이 방법을 사용하게 위해서는 도함수 $ f’(x) $를 구해야 합니다. 프로그래밍을 통해 도함수를 구하는 방법은 함수의 미분에서 다루고 있습니다.
\[\begin {align*} f_1(x) &= 3x \\ f_2(x) &= \cos {x} \end {align*}\]위의 두 함수가 만나는 점을 찾으려고 합니다. 두 점이 만나는 지점은 아래와 같은 방법으로 구할 수 있습니다.
\[\begin {align*} 0 &= f_1 (x) - f_2 (x) \\ &= 3x - \cos x \end {align*}\]이런 형태의 다항식을 만들고 $ x $를 찾는 것이 뉴턴 방법으로 해결하는 문제의 기본 형태입니다. 위 다항식에서 임의의 초기값 $ x_0 $를 사용하여 $f(x_0)$와 $f’(x_0)$를 구합니다.
\[\begin {align*} f(x_0) &= 3x_0 - \cos x_0 \\ f'(x_0) &= 3 + \sin x_0 \end {align*}\]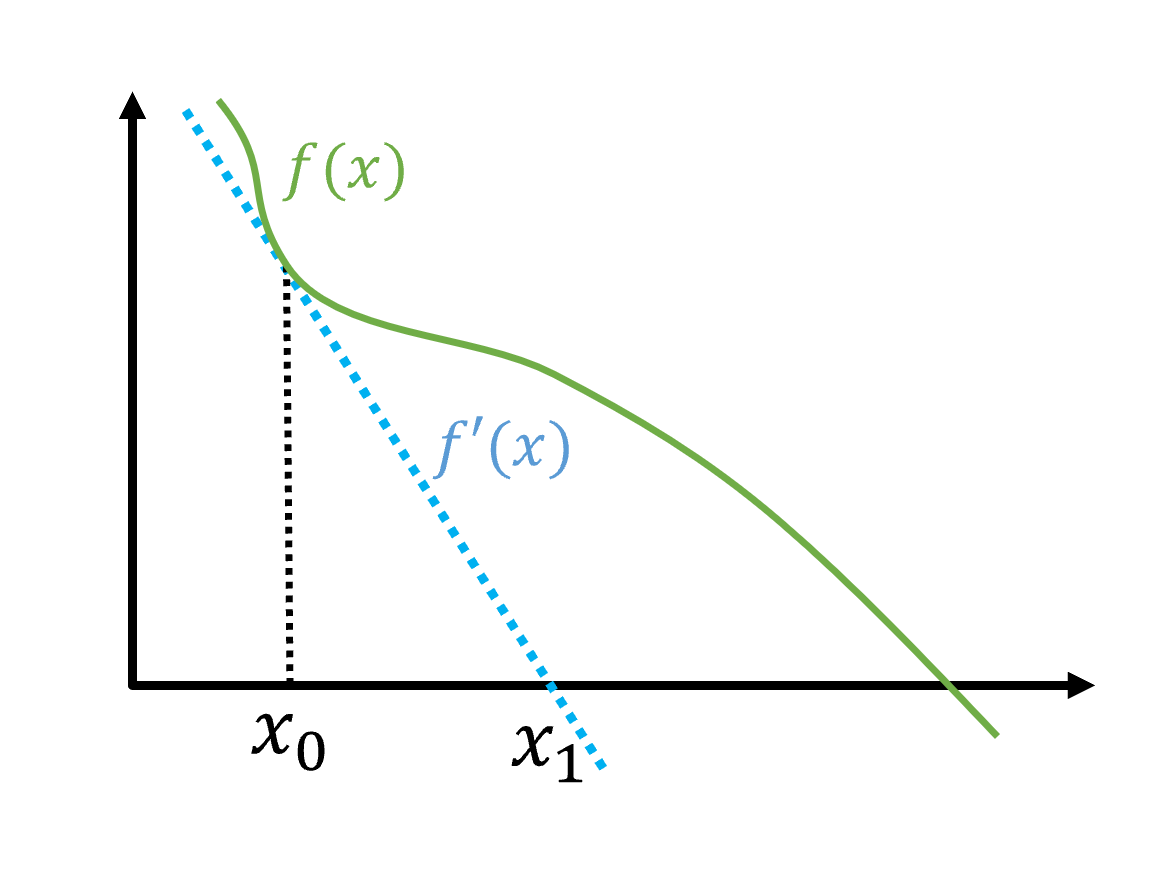
그래프를 그린다고 생각하면, $f’(x_0)$는 ($x_0$, $f(x_0)$) 지점과 접한 접선의 기울기입니다. $ x_1 $은 접선과 우리가 목표하는 지점인 $f(x)=0$이 만나는 점으로 하면 다음과 같이 쓸 수 있습니다.
이 식을 정리하면,
\[x_1 = x_0 - \frac {f(x_0)} {f'(x_0)}\]이 됩니다. 뉴턴 방법은 이렇게 도함수의 성질을 이용해 $f(x) = 0$인 $x$를 찾아냅니다.
파이썬으로 뉴턴 방법 사용하기
1
2
3
4
5
6
7
8
9
10
import numpy as np
def f(x):
return 3 * x - np.cos(x)
def df(x):
return 3 + np.sin(x)
def newton_method(x0, f, df):
return x0 - (f(x0) / df(x0))
프로그래밍을 통해 함수와 도함수를 대입하여 newton_method()를 충분히 반복하여 해를 찾습니다. 그림은 우리가 구하려고 하는 두 함수의 모양과 뉴턴 방법으로 찾아낸 $x$값을 아래에서 위로 표시한 것입니다.
과제: 충분한 반복 기준 만들기
뉴턴 방법의 점화식,
\[x_n = x_{n-1} - \frac {f(x_{n-1})} {f'(x_{n-1})}\]에서 $ f(x_{n-1}) / f’(x_{n-1}) $ 항은 $ x_n $과 $ x_{n-1} $사이의 변화량을 의미하며 시행을 반복할수록 감소합니다. 이 갚이 충분히 작아질때까지 반복하는 프로그램을 만들어봅시다.
과제: 뉴턴 방법의 약점
뉴턴 방법은 해석적으로 해를 구하는게 매우 어렵거나 사실상 불가능하다고 하더라도 미분만 가능하다면 해를 구할 수 있습니다. 하지만 약점도 있는데요. 뉴턴 방법으로 다음 식의 해를 찾아봅시다.
\[\sin x + 3x^2 - 2 = 0\]여기서 $ x_0 = -0.5 $, $ x_0 = 0.5 $를 넣어 해를 구해봅시다. 결과를 통해 뉴턴 방법이 가지고 있는 약점을 생각해봅시다.
룽게-쿠타 방법
룽게-쿠타 방법(Runge–Kutta method)은 초기값을 가지고 있는 운동에 대해 쓸 수 있는 방법입니다. 여기서는 일반적으로 사용하는 4차 룽게 쿠타 방법을 소개합니다. 초기값이 다음과 같을 때,
\[f(t_0) = x_0\]룽게-쿠타 방법의 점화식은 다음과 같습니다. ($n = 0,1,2,…$)
\[x_{n+1} = x_n + h \frac {k_1 + 2 k_2 + 2 k_3 + k_4} {6}\]$k$는 각각 아래와 같이 계산합니다.
\[\begin {align*} k_1 &= f(t_n, x_n) \\ k_2 &= f(t_n + \frac {h} {2}, x_n + \frac {h k_1} {2} ) \\ k_3 &= f(t_n + \frac {h} {2}, x_n + \frac {h k_2} {2} ) \\ k_4 &= f(t_n + h, x_n + h k_3 ) \end {align*}\]의 점화식을 얻습니다. 여기서 $ h $는 0보다 큰 충분히 작은 값입니다. 처음 값의 기울기와 끝 값의 기울기, 각각의 중간에 해당하는 기울기를 이용해서 정확도를 높이는 방법입니다.
룽게-쿠타 함수
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def RK_method(func, x0, t0, t1, h=0.01):
"""룽게-쿠타 방법
func: 함수(t, x)
x0: x 초기값
t0, t1, h: 시간의 시작값, 끝값, 간격
"""
time = np.arange(t0, t1, h)
x = np.zeros(time.shape)
x[0] = x0
for idx in range(1, x.shape[0]):
k1 = func(time[idx - 1], x[idx - 1])
k2 = func(time[idx - 1] + h / 2, x[idx - 1] + k1 / 2)
k3 = func(time[idx - 1] + h / 2, x[idx - 1] + k2 / 2)
k4 = func(time[idx - 1] + h, x[idx - 1] + k3)
dx = (k1 + 2 * k2 + 2 * k3 + k4) * h / 6
x[idx] = x[idx - 1] + dx
return time, x
예제: 준비중
여러 입자의 운동
뉴턴의 프린키피아에서 태양, 지구 그리고 달의 세 천체에 대한 궤도를 그리는 문제로 시작한 삼체 문제(3-body problem)는 이후 앙리 푸앵카레에 의해 일반해가 불가능하다는 것을 증명할 때까지 많은 사람들이 빠져들었던 난제 중 하나였습니다.
여기서는 삼체문제를 확장하여 중력을 주고받는 N개의 입자가 어떤 궤도를 그리는지 알아내기 위해 벌렛(verlet) 방법을 사용합니다.
다체문제
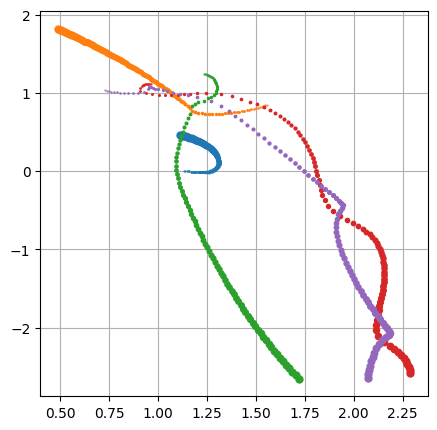
N개의 입자가 중력을 주고받는 상황에서 각 입자가 그리는 궤적을 추적합니다. 벌렛 방법으로 기술하는 각 입자의 운동방정식은 이렇게 쓰입니다.
\[\begin{align} x(t_{i+1}) &= x(t_i) + v(t_i)h + \frac{1}{2} a(t_i)h^2 \\ v(t_{i+1}) &= v(t) + \frac{a(t_{i+1}) + a(t_i)}{2} h \end{align} \\ h = t_{i+1} - t_i\]벌렛 방법은 아래 과정을 거칩니다.
- $ t_0 = 0 $일 때의 초기값 $ x(0) $과 $ v(0) $, 시간 간격 $ h $를 설정합니다.
- $ t_1 = t_0 + h $ 일 때의 식 (1)을 풀어 $x_1$을 얻습니다.
- 새로운 위치 $x_1$으로부터 $ a(t_1) $을 구합니다.
- 앞서 구한 $ a(t_1) $를 이용해 식(2)를 풀어 저장합니다.
- $ t_i $의 $ i $를 증가시키면서 원하는 만큼 2~4를 반복합니다.
그림은 5개의 입자가 무작위로 배치된 뒤, 무작위의 속도를 가지고 운동하는 궤적을 그린 것입니다.
위치와 속도의 점화식
1
2
3
4
5
def verlet_x(x, v, a):
"""위치 점화식"""
dx = v * h + 0.5 * a * h ** 2
return x + dx
1
2
3
4
def verlet_v(v, a):
"""속도 점화식"""
dv = a * h
return v + dv
두 함수는 각각 벌렛 절차에 사용하는 $ x(t_{i+1}) $과 $ v(t_{i+1}) $입니다.
주고받는 중력으로부터 가속 계산
1
2
3
4
5
6
7
def acceleration(xy1, xy2, m2):
"""중력을 계산하고 가속도로 출력"""
r_sq = (xy2[0] - xy1[0]) ** 2 + (xy2[1] - xy1[1]) ** 2
theta = np.arctan2(xy2[1] - xy1[1], xy2[0] - xy1[0])
force = m2 / r_sq
return np.array([force * np.cos(theta), force * np.sin(theta)])
이 함수는 두 입자 사이의 힘과 가속도를 계산합니다. 영향을 받는 입자의 위치 xy1과 영향을 주는 입자의 위치 xy2는 np.array([x, y])형태의 벡터입니다.
입자 1과 입자 n사이의 중력으로 인한 가속는 다음과 같고,
\[a_n(\vec {r}_1, \vec {r}_n, t_{i+1}) = - \frac {m_n (\vec {r}_{1} - \vec {r}_{n}) } {|\vec {r}_{1} - \vec {r}_{n}|^3}\]이 식이 acceleration()함수와 같은역할을 합니다. 벌렛 모사에 필요한 입자 1에 작용하는 총 가속도는 이렇게 쓸 수 있습니다.
벌렛으로 궤도 구하기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def particle_motion(time, pos=[], vel=[], mass=[]):
"""벌렛 방법으로 입자의 궤도를 작성"""
# 위치와 속도 배열 초기화
pos_arr, vel_arr = [], []
for _pos, _vel in zip(pos, vel):
vel_arr.append(np.zeros([time.shape[0], 2]))
pos_arr.append(np.zeros([time.shape[0], 2]))
pos_arr[-1][0, :] = _pos
vel_arr[-1][0, :] = _vel
# 운동 배열 채우기
# idx는 t_n의 n을 의미
for idx in range(1, time.shape[0]):
# num: 입자 번호, pos: 입자 위치, vel: 입자 속도
for num, pos, vel in zip(range(len(pos_arr)), pos_arr, vel_arr):
# acc0: 움직이기 전 가속도
acc0 = np.zeros(2)
for pidx in [i for i in range(len(pos_arr)) if i != num]:
m2 = mass[pidx]
xy1 = pos[idx - 1]
xy2 = pos_arr[pidx][idx - 1]
acc0 += acceleration(xy1, xy2, m2)
pos[idx, :] = verlet_x(pos[idx - 1], vel[idx - 1], acc0)
# acc1: 움직인 후의 가속도
acc1 = np.zeros(2)
for pidx in [i for i in range(len(pos_arr)) if i != num]:
m2 = mass[pidx]
xy1 = pos[idx]
xy2 = pos_arr[pidx][idx]
acc1 += acceleration(xy1, xy2, m2)
vel[idx, :] = verlet_v(vel[idx - 1], (acc0 + acc1) / 2)
return pos_arr
particle_motion 함수는 벌렛 모사를 실행하는 부분입니다. 함수는 아래 과정을 재현하고 있습니다.
- $ t_0 = 0 $일 때의 초기값 $ x(0) $과 $ v(0) $, 시간 간격 $ h $를 설정합니다.
- $ t_1 = t_0 + h $ 일 때의 식 (1)을 풀어 $x_1$을 얻습니다.
- 새로운 위치 $x_1$으로부터 $ a(t_1) $을 구합니다.
- 앞서 구한 $ a(t_1) $를 이용해 식(2)를 풀어 저장합니다.
- $ t_i $의 $ i $를 증가시키면서 원하는 만큼 2~4를 반복합니다.
과제: 지구, 달, 태양의 궤적 모사하기
지구와 태양, 달이 있을 때 한 순간의 위치와 속도를 대입하고 각각의 질량을 초기화변수에 두어 위의 벌렛 알고리즘을 실행합니다. 단, 위의 acceleration()의 force변수에는 중력 상수를 적용하지 않았으므로 이를 수정한 뒤 시행해야 합니다.
몬테카를로 방법
몬테카를로 방법은 난수(무작위로 뽑은 수)를 활용하여 누적되는 결과값을 모아 결과의 분포를 계산하거나 복잡한 함수의 값을 계산하는데 쓰입니다.
파이 근사하기
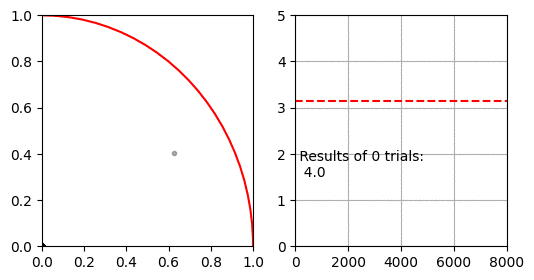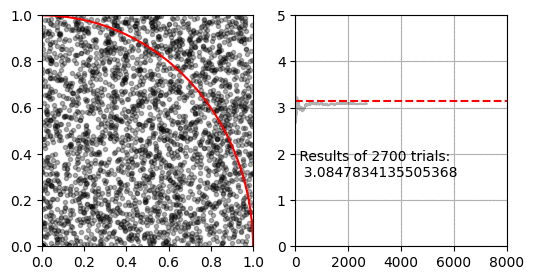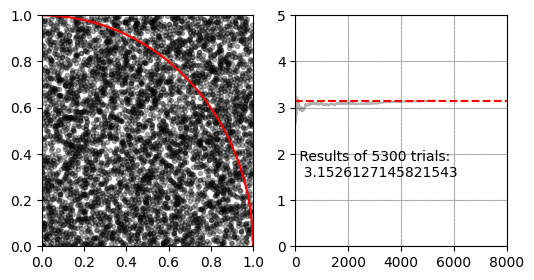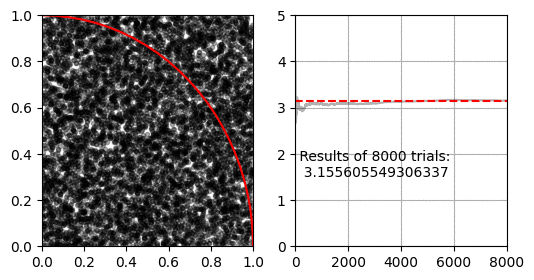
몬테카를로 적분을 이용해 $\pi$를 구하는 방법입니다. 이 방법은 유한한 공간에서 난수로 생성한 점이 적분할 공간 안에 있는지 밖에 있는지 확인 할 수 있는 경우에 사용할 수 있습니다.
먼저 $x=[0, 1], y=[0,1]$인 공간이 있습니다. 이 공간에 중심이 $(0, 0)$이고 반지름이 $1$인 사분원이 있습니다. 사분원과 사각형의 넓이 비율은 $ \pi r^2 / 4 r^2 $ 이므로 반지름 1인 사분원과 한 변이 1인 직사각형의 비율은 $ \pi / 4 $가 됩니다.
몬테카를로 적분은 난수로 생성한 점 $(x, y)$이 $ x^2 + y^2 < 1 $을 만족하면 사분원 안에 있는 것으로 판단하여, 전체 생성한 난수 점(정사각형의 넓이)과 사분원 내의 난수 점(사분원의 넓이)의 비율로 $\pi$를 추정합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import numpy as np
count_lim = 8001
points = np.zeros([count_lim, 2])
calc_pi = np.zeros([count_lim, 2])
result_pi = 0.0
inner = 0
for count in range(count_lim):
points[count, :] = pos = np.random.rand(2)
if np.sum(pos ** 2) < 1:
inner += 1
result_pi = 4 * inner / (count + 1)
calc_pi[count, :] = count + 1, result_pi
if count % 100 == 0:
print(f"Monte carlo progress: {count} / {count_lim}")
방사성 붕괴
특정한 단위시간당 붕괴 확률을 가진 입자들이 모여있을 때 전체 핵종의 수가 어떻게 변화하는지를 몬테카를로 방법으로 추정합니다.
1
2
3
4
5
6
import numpy as np
def decay_event(nuclides, probability):
"""붕괴 단일 이벤트"""
func = lambda x: 1 if np.random.rand() > probability and x > 0 else 0
return np.vectorize(func)(nuclides)
np.ones()로 초기화한 배열을 다룬다는 가정을 두고 맵핑(mapping)이라는 방법을 사용하여 각 입자에 독립적인 확률로 붕괴하도록 하는 사건을 적용합니다. 일반 함수 func()를 람다식 문법으로 생성한 후 이를 numpy.array를 위한 맵핑 함수로 변경하기 위해 np.vectorize(func)를 씁니다.
np.vectorize(func)의 결과 또란 함수이므로 괄호를 붙여 이벤트를 적용할 배열을 매개변수로 전달하기 때문에 np.vectorize(func)(nuclides)처럼 괄호가 연달아 나오는 생소한 문법이 되었지만 잘 작동합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import matplotlib.pyplot as plt
import numpy as np
nuclides_n = 500 # 핵종의 수
probability = 0.01 # 단위시간당 붕괴 확률
time_max = 300 # 관측 시간
nuclides = np.ones(nuclides_n)
x = np.arange(time_max)
y = []
for i in x:
y.append(np.sum(nuclides))
nuclides = decay_event(nuclides, probability)
plt.bar(x, y, 1, color="#AAA")
plt.plot(x, nuclides_n * np.exp(-probability * x), "r--")
plt.xlabel("Time")
plt.ylabel("Number of nuclides")
plt.xlim(0, time_max)
plt.ylim(0, nuclides_n)
plt.show()
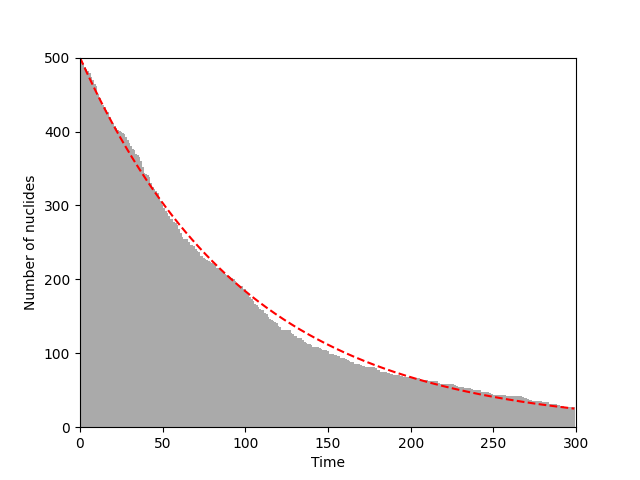
이벤트를 반복하고 결과를 그래프로 출력하는 부분입니다.
nuclides 변수는 np.ones()로 초기화한 배열이 들어 있으며, 이렇게 생성한 배열은 원소의 값이 모두 1로 채워져 있습니다. 즉, 핵종이 붕괴했으면 원소의 값이 0, 붕괴하지 않았으면 원소의 값이 1을 가지도록 구현하였습니다. 이러한 구현은 나중에 남은 원소의 수를 구하려고 할 때 np.sum()을 사용해서 간단하게 구할 수 있으므로 유용합니다.
매 시간마다 남은 원소의 수와 함께 이론적으로 유도한 방사성 붕괴 공식 $ N(t) = N(0) e^{-\lambda t} $을 빨간 점선으로 표시하였습니다. 독립적인 붕괴 확률에 따라 붕괴 하는 핵종들의 수가 수학적으로 유도한 수식과 잘 맞는 것을 볼 수 있습니다.
몬티 홀 문제
참가자는 세개의 문 중에 하나를 선택하여 문 뒤에 숨겨진 선물을 획득할 수 있습니다. 셋 중 하나의 문 뒤에는 자동차가 있고 나머지 두 개의 문에는 염소가 있습니다. 이 때 참가자가 자동차가 숨겨진 문을 선택할 확률은 1/3일 것입니다. 그런데 여기서 사회자는 염소가 들어있는 하나의 문을 열어서 보여주고 선택을 바꿀것인지 묻습니다. 선택을 바꾸거나 바꾸지 않아도 참가자가 자동차를 뽑을은 1/2일까요?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import numpy as np
count = 1000 # 시행 수
doors = ["A", "B", "C"] # 문
def monty_hall(count, doors, has_change=True):
player = np.zeros(count)
for idx in range(count):
car = np.random.choice(doors)
# 첫 번째 선택
choice = np.random.choice(doors)
# 사회자가 염소를 보여줌
goats = doors.copy()
goats.remove(car)
try:
goats.remove(choice)
except:
pass
show = np.random.choice(goats)
selection = doors.copy()
selection.remove(show)
# 선택을 변경할지 말지 결정
if has_change:
selection.remove(choice)
last = np.random.choice(selection)
else:
last = choice
print(
f'{idx: 4d} Show [{"Success" if last == car else " Failed"}]: '
f'choice "{choice}", Show goat "{show}", Car in "{car}"'
)
player[idx] = 1 if last == car else 0
return player
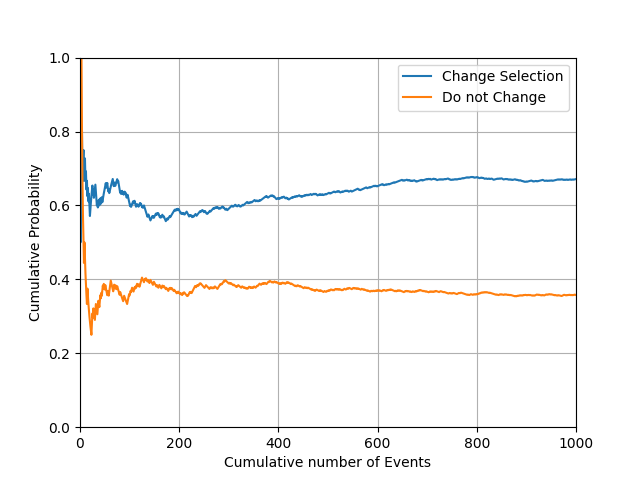
X축은 누적 시행 횟수, Y축은 누적 상품 획득률입니다. 시행횟수가 증가할수록 특정 수치에 수렴하는 것을 볼 수 있습니다.
재미있게도 중간에 사회자가 개입했을 뿐 최종 선택은 그저 1/2의 확률 문제인줄 알았던 게임이었는데, 오히려 선택을 바꾸느냐 아니냐에 따라 확률이 바뀌고 선택을 바꾸는 것이 오히려 유리한 것을 볼 수 있습니다.
여기서 소개한 몬티 홀 문제(Monty Hall problem)는 베이즈 정리가 해결하는 대표적인 문제 중 하나입니다. 베이즈 정리를 통해 수학적이고 논리적인 해결 방법을 얻을 수 있습니다.
최적화
개미집단 최적화
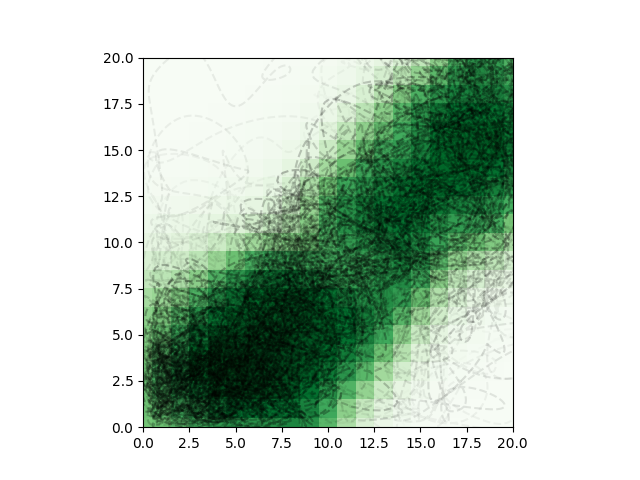
개미집단 최적화(Ant colony optimization)는 개미가 먹이와 집의 경로를 찾는 과정을 흉내내어 최적의 경로를 찾아내는 최적화 기법입니다. 이런 경우에 유용하게 사용할 수 있습니다.
- 답이 하나가 아닌 경우
- 답이 여러개일 가능성이 있는 경우
해결할 수 있는 문제의 특징은 이렇습니다.
- 출발지와 목적지가 있음(혹은 출발지로 되돌아옴)
- 출발지와 도착지 사이에는 경로가 존재함
- 노드와 경로의 수는 유한하며 이미 알고 있음
여기서는 사각형 격자 공간에서 시작과 골 지점이 있는 상황을 두고 개미집단 최적화를 사용합니다.
프로그램 구조
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import matplotlib.pyplot as plt
import numpy as np
area = np.ones([20, 20]) # 지역 생성
start = (1, 1) # 개미 출발지점
goal = (19, 14) # 도착해야 하는 지점
path_count = 40 # 경로를 만들 개미 수
path_max_len = 20 * 20 # 최대 경로 길이
pheromone = 1.0 # 페로몬 가산치
volatility = 0.3 # 스탭 당 페로몬 휘발율
def get_neighbors(x, y):
"""x, y와 이웃한 좌표 목록 출력"""
def ant_path_finding():
"""개미 경로 생성"""
def step_end(path):
"""경로를 따라 페로몬을 더하고 전 지역의 페로몬을 한번 휘발시킴"""
if __name__ == "__main__":
# 계산 및 그래프 작성
이웃한 좌표 찾기
1
2
3
4
5
6
7
8
9
def get_neighbors(x, y):
"""x, y와 이웃한 좌표 목록 출력"""
max_x, max_y = area.shape
return [
(i, j)
for i in range(x - 1, x + 2)
for j in range(y - 1, y + 2)
if (i != x or j != y) and (i >= 0 and j >= 0) and (i < max_x and j < max_y)
]
현재 타일 좌표를 x, y로 받아 상하좌우와 대간선 방향까지 감안한(8방향) 이웃 타일들의 좌표를 출력합니다.
개미 경로 생성
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def ant_path_finding():
"""개미 경로 생성"""
path = [start]
x, y = start
count = 0
while x != goal[0] or y != goal[1]:
count += 1
if count > 400:
return None
neighbors = get_neighbors(x, y)
values = np.array([area[i, j] for i, j in neighbors])
p = values / np.sum(values)
x, y = neighbors[np.random.choice(len(neighbors), p=p)]
while (x, y) == path[-1]:
x, y = neighbors[np.random.choice(len(neighbors), p=p)]
path.append((x, y))
return path
개미 한 마리가 페로몬의 농도로 보정한 확률 공간에 따라 8방향 중 하나를 골라 이동합니다. 400번 이동할 때까지 골 지점에 도착하지 못하면 이동을 포기합니다.
지역 페로몬 업데이트
1
2
3
4
5
6
7
8
9
def step_end(path):
"""경로를 따라 페로몬을 더하고 전 지역의 페로몬을 한번 휘발시킴"""
global area
if path is None:
return
for x, y in set(path):
area[x, y] += pheromone / len(set(path))
area[:, :] = area * (1 - volatility)
return
골 지점에 성공적으로 도착한 개미의 경로를 따라 페로몬을 더하고 타일 전체의 페로몬을 정해진 비율로 휘발시킵니다.
더 멋지게 만들기
이런 아이디어를 추가하면 더 멋진 결과를 얻을 수 있습니다.
- B-스플라인 곡선을 사용해서 개미의 경로를 부드럽게 만들어 줄 수 있습니다. 당장의 계산 결에는 영향을 미치지 않겠지만 실제 개미의 움직임에 더 가까운 그래프를 얻을 수 있습니다.
- 가우시안 필터를 사용해서 페로몬이 이웃한 지역으로 부드럽게 확산되는 것을 계산에 추가할 수 있습니다. 경로가 고정되는 것을 조금 더 효율적으로 늦춰줄 수 있습니다.
- 예제는 주어진 횟수만큼 반복했지만 조건부 반복(
while)을 사용해서 경로가 충분히 고정되었거나 페로몬의 변화가 충분히 적을 때 계산을 종료하도록 만들 수 있습니다.
이외에도 생각나는게 있다면 직접 프로그램을 수정해서 더 멋진 결과를 얻어 봅시다.