뉴턴 방법
여기서는 뉴턴 방법(Newton method)을 이용해 해를 찾는 방법과 운동하는 물체의 경로를 찾는 방법을 알아봅니다.
뉴턴 방법으로 해 찾기
뉴턴 방법(Newton method)은 아래와 같은 점화식을 가집니다.
\[x_n = x_{n-1} - \frac {f(x_{n-1})} {f'(x_{n-1})}\]이 점화식을 반복할수록 극한값을 가지는 $x_n$에 수렴하게 될 것입니다. 이 방법을 사용하게 위해서는 도함수 $ f’(x) $를 구해야 합니다. 프로그래밍을 통해 도함수를 구하는 방법은 함수의 미분에서 다루고 있습니다.
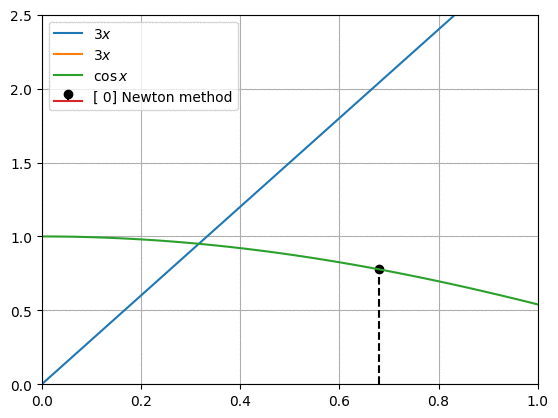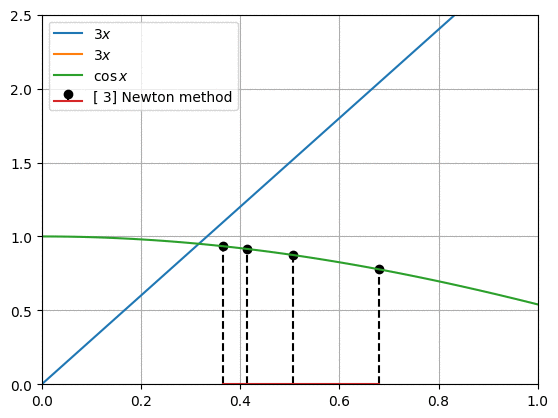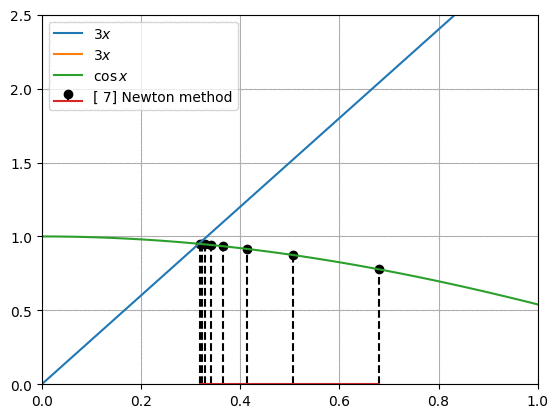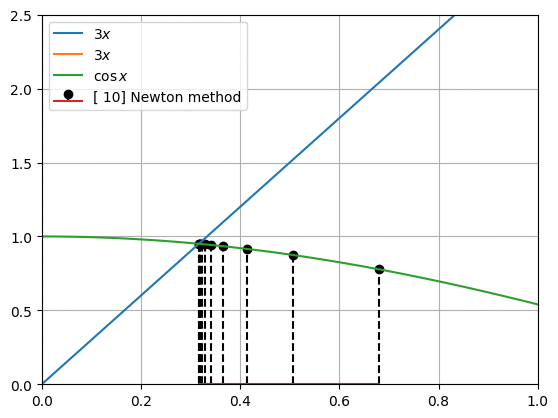
\[\begin {align*} f_1(x) &= 3x \\ f_2(x) &= \cos {x} \end {align*}\]위의 두 함수가 만나는 점을 찾으려고 합니다. 두 점이 만나는 지점은 아래와 같은 방법으로 구할 수 있습니다.
\[\begin {align*} 0 &= f_1 (x) - f_2 (x) \\ &= 3x - \cos x \end {align*}\]이런 형태의 다항식을 만들고 $ x $를 찾는 것이 뉴턴 방법으로 해결하는 문제의 기본 형태입니다. 위 다항식에서 임의의 초기값 $ x_0 $를 사용하여 $f(x_0)$와 $f’(x_0)$를 구합니다.
\[\begin {align*} f(x_0) &= 3x_0 - \cos x_0 \\ f'(x_0) &= 3 + \sin x_0 \end {align*}\]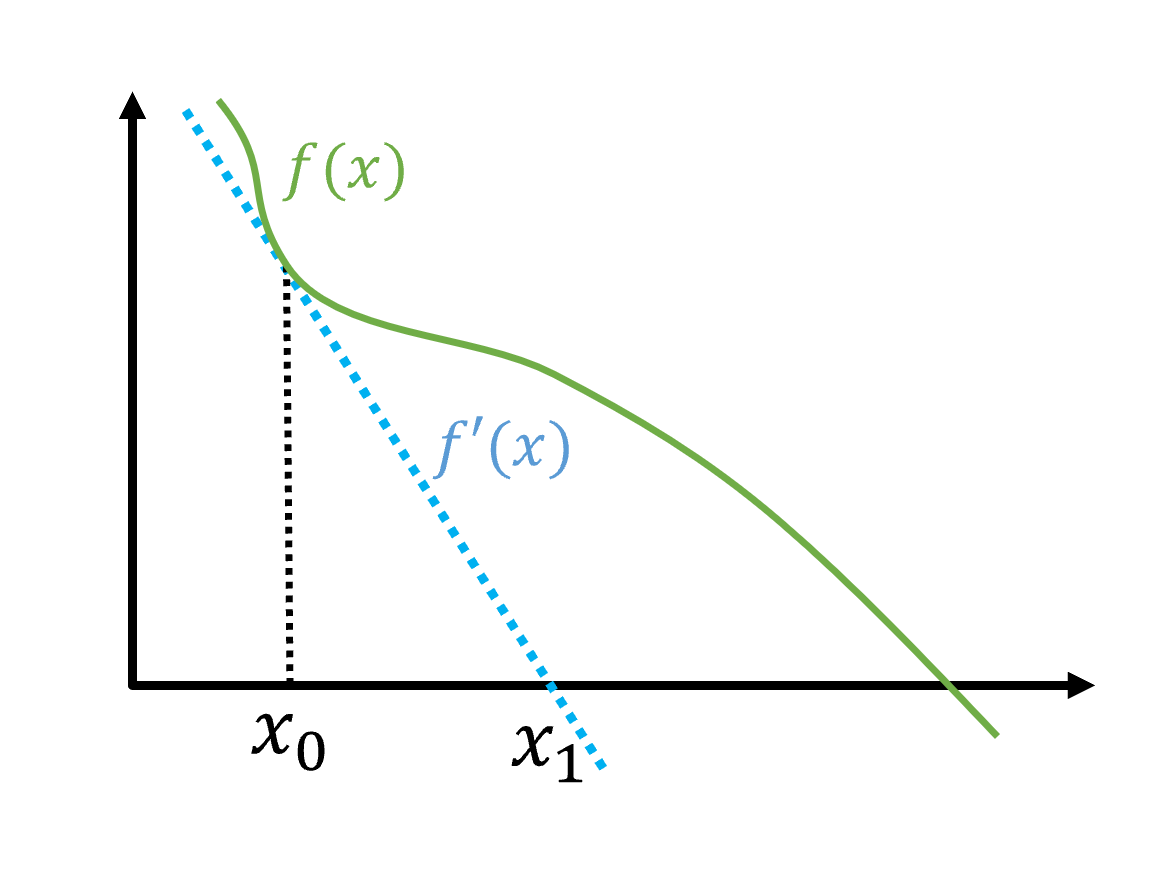
그래프를 그린다고 생각하면, $f’(x_0)$는 ($x_0$, $f(x_0)$) 지점과 접한 접선의 기울기입니다. $ x_1 $은 접선과 우리가 목표하는 지점인 $f(x)=0$이 만나는 점으로 하면 다음과 같이 쓸 수 있습니다.
이 식을 정리하면,
\[x_1 = x_0 - \frac {f(x_0)} {f'(x_0)}\]이 됩니다. 뉴턴 방법은 이렇게 도함수의 성질을 이용해 $f(x) = 0$인 $x$를 찾아냅니다.
파이썬으로 뉴턴 방법 사용하기
1
2
3
4
5
6
7
8
9
10
import numpy as np
def f(x):
return 3 * x - np.cos(x)
def df(x):
return 3 + np.sin(x)
def newton_method(x0, f, df):
return x0 - (f(x0) / df(x0))
프로그래밍을 통해 함수와 도함수를 대입하여 newton_method()를 충분히 반복하여 해를 찾습니다. 그림은 우리가 구하려고 하는 두 함수의 모양과 뉴턴 방법으로 찾아낸 $x$값을 아래에서 위로 표시한 것입니다.
과제: 충분한 반복 기준 만들기
뉴턴 방법의 점화식,
\[x_n = x_{n-1} - \frac {f(x_{n-1})} {f'(x_{n-1})}\]에서 $ f(x_{n-1}) / f’(x_{n-1}) $ 항은 $ x_n $과 $ x_{n-1} $사이의 변화량을 의미하며 시행을 반복할수록 감소합니다. 이 갚이 충분히 작아질때까지 반복하는 프로그램을 만들어봅시다.
과제: 뉴턴 방법의 약점
뉴턴 방법은 해석적으로 해를 구하는게 매우 어렵거나 사실상 불가능하다고 하더라도 미분만 가능하다면 해를 구할 수 있습니다. 하지만 약점도 있는데요. 뉴턴 방법으로 다음 식의 해를 찾아봅시다.
\[\sin x + 3x^2 - 2 = 0\]여기서 $ x_0 = -0.5 $, $ x_0 = 0.5 $를 넣어 해를 구해봅시다. 결과를 통해 뉴턴 방법이 가지고 있는 약점을 생각해봅시다.