개미집단 최적화
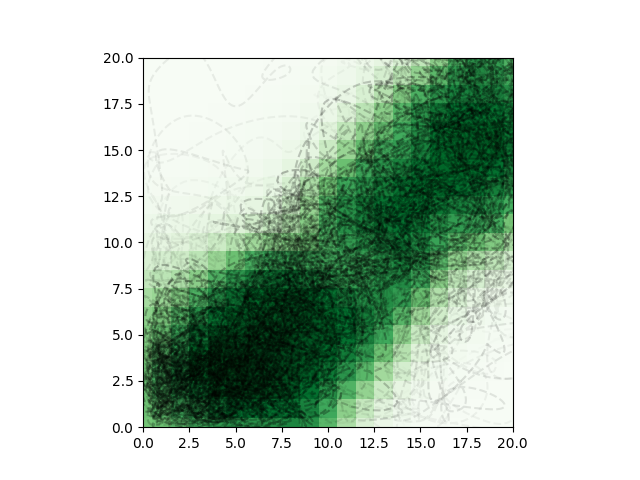
개미집단 최적화(Ant colony optimization)는 개미가 먹이와 집의 경로를 찾는 과정을 흉내내어 최적의 경로를 찾아내는 최적화 기법입니다. 이런 경우에 유용하게 사용할 수 있습니다.
- 답이 하나가 아닌 경우
- 답이 여러개일 가능성이 있는 경우
해결할 수 있는 문제의 특징은 이렇습니다.
- 출발지와 목적지가 있음(혹은 출발지로 되돌아옴)
- 출발지와 도착지 사이에는 경로가 존재함
- 노드와 경로의 수는 유한하며 이미 알고 있음
여기서는 사각형 격자 공간에서 시작과 골 지점이 있는 상황을 두고 개미집단 최적화를 사용합니다.
프로그램 구조
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import matplotlib.pyplot as plt
import numpy as np
area = np.ones([20, 20]) # 지역 생성
start = (1, 1) # 개미 출발지점
goal = (19, 14) # 도착해야 하는 지점
path_count = 40 # 경로를 만들 개미 수
path_max_len = 20 * 20 # 최대 경로 길이
pheromone = 1.0 # 페로몬 가산치
volatility = 0.3 # 스탭 당 페로몬 휘발율
def get_neighbors(x, y):
"""x, y와 이웃한 좌표 목록 출력"""
def ant_path_finding():
"""개미 경로 생성"""
def step_end(path):
"""경로를 따라 페로몬을 더하고 전 지역의 페로몬을 한번 휘발시킴"""
if __name__ == "__main__":
# 계산 및 그래프 작성
이웃한 좌표 찾기
1
2
3
4
5
6
7
8
9
def get_neighbors(x, y):
"""x, y와 이웃한 좌표 목록 출력"""
max_x, max_y = area.shape
return [
(i, j)
for i in range(x - 1, x + 2)
for j in range(y - 1, y + 2)
if (i != x or j != y) and (i >= 0 and j >= 0) and (i < max_x and j < max_y)
]
현재 타일 좌표를 x, y로 받아 상하좌우와 대간선 방향까지 감안한(8방향) 이웃 타일들의 좌표를 출력합니다.
개미 경로 생성
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def ant_path_finding():
"""개미 경로 생성"""
path = [start]
x, y = start
count = 0
while x != goal[0] or y != goal[1]:
count += 1
if count > 400:
return None
neighbors = get_neighbors(x, y)
values = np.array([area[i, j] for i, j in neighbors])
p = values / np.sum(values)
x, y = neighbors[np.random.choice(len(neighbors), p=p)]
while (x, y) == path[-1]:
x, y = neighbors[np.random.choice(len(neighbors), p=p)]
path.append((x, y))
return path
개미 한 마리가 페로몬의 농도로 보정한 확률 공간에 따라 8방향 중 하나를 골라 이동합니다. 400번 이동할 때까지 골 지점에 도착하지 못하면 이동을 포기합니다.
지역 페로몬 업데이트
1
2
3
4
5
6
7
8
9
def step_end(path):
"""경로를 따라 페로몬을 더하고 전 지역의 페로몬을 한번 휘발시킴"""
global area
if path is None:
return
for x, y in set(path):
area[x, y] += pheromone / len(set(path))
area[:, :] = area * (1 - volatility)
return
골 지점에 성공적으로 도착한 개미의 경로를 따라 페로몬을 더하고 타일 전체의 페로몬을 정해진 비율로 휘발시킵니다.
더 멋지게 만들기
이런 아이디어를 추가하면 더 멋진 결과를 얻을 수 있습니다.
- B-스플라인 곡선을 사용해서 개미의 경로를 부드럽게 만들어 줄 수 있습니다. 당장의 계산 결에는 영향을 미치지 않겠지만 실제 개미의 움직임에 더 가까운 그래프를 얻을 수 있습니다.
- 가우시안 필터를 사용해서 페로몬이 이웃한 지역으로 부드럽게 확산되는 것을 계산에 추가할 수 있습니다. 경로가 고정되는 것을 조금 더 효율적으로 늦춰줄 수 있습니다.
- 예제는 주어진 횟수만큼 반복했지만 조건부 반복(
while)을 사용해서 경로가 충분히 고정되었거나 페로몬의 변화가 충분히 적을 때 계산을 종료하도록 만들 수 있습니다.
이외에도 생각나는게 있다면 직접 프로그램을 수정해서 더 멋진 결과를 얻어 봅시다.