함수의 적분

함수를 구간적분하고 적분 값과 적분 구간을 그래프에 표시합니다.

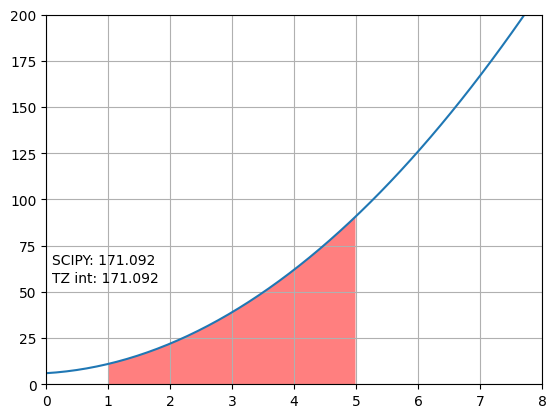
이 프로그램은 사다리꼴 적분을 직접 int_f() 함수로 구현해서 사용하는 방법과 scipy의 integrate.trapezoid함수를 이용하는 방법을 각각 실행하고 결과를 그래프상에 표시합니다.

그림의 SCIPY는 scipy에서 제공하는 적분함수 trapezoid()로 계산한 적분량, TZ int는 직접 만든 int_f()로 계산한 적분량입니다. 적분 영역은 빨간색으로 표시하였습니다.

• 실습 파일: 03_analysis/04_function_integration.py

사다리꼴 적분

1
2
3
4
5
6
def int_f(func, x_min, x_max, h):
    output = 0
    x = np.arange(x_min, x_max, h)
    for idx in range(len(x) - 1):
        output += (func(x[idx]) + func(x[idx + 1])) * h / 2
    return output

를 함수로 구현한 부분입니다. h는 $ \text {d} x $, func는 $ f(x) $, x_min과 x_max는 적분 구간을 나타냅니다.

채워진 곡선 그리기

1
2
3
4
5
6
7
8
x_inf = np.arange(min_x, max_x, h)
y_inf = f(x_inf)
x_inf = np.concatenate(([x_inf[0]], x_inf, [x_inf[-1]]))
y_inf = np.concatenate(([0], y_inf, [0]))

plt.fill(x_inf, y_inf, "r", alpha=0.5)
plt.grid(True)
plt.show()

plt.fill()은 채워진 곡선을 얻고자 할 때 씁니다. 곡선을 가장 적은 넓이로 닫을 수 있는 도형을 택하기 때문에 종종 원하지 않는 결과가 나오기도 합니다. 이를 해결하기 위해 np.concatenate()을 사용하여 생길 도형을 강제시킵니다.

np.concatenate((a, b, c))는 배열 a, b, c를 순서대로 붙인 배열을 출력합니다.

plt.fill()에서 사용한 "r"과 alpha=0.5는 각각 빨강으로 채우되 투명도는 50%로 할 것을 지시합니다.