toc

데이터의 적분

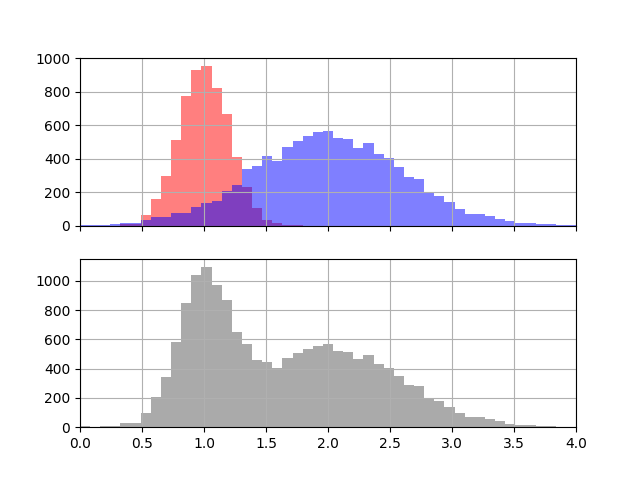
데이터 적분 1

그림은 가상의 반응에 의해 발생한 입자 A(빨강)와 B(파랑)의 에너지 스펙트럼 입니다. 반응이 일어나는 환경에서 일정 시간동안 입사하는 입자의 에너지를 측정하여 히스토그램 형태로 표시하였습니다. 그림 상단은 각 입자의 스펙트럼, 하단은 실제로 얻게 될 스펙트럼입니다.

실제 실험에서 우리는 아래의 데이터만을 얻게 됩니다. 서로 다른 운동 예너지를 가진 두 종류의 입자를 검출했다는 사실 정도만 알 수 있습니다.

여기서 우리는 가상의 반응이 지닌 특성을 알아내기 위해 가상의 반응이 생성하는 입자 A와 입자 B의 비율을 알고 싶습니다.

데이터 형식

주어진 데이터는 아래와 같은 형식을 가지고 있습니다. 데이터를 쉼표로 구분하는 것은 csv형식의 특징입니다. 1열은 에너지 채널의 최소값을 의미하고, 2열은 측정시간동안 채널에 해당하는 입자가 몇 개 측정되었는지를 나타냅니다.

0.0000, 6
0.0816, 4
0.1633, 5
0.2449, 8
0.3265, 26
0.4082, 28
0.4898, 95
0.5714, 209
...

파일을 읽어들여 각각 bins와 count에 넣어둡니다.

1
2
3
4
5
6

bins, count = [], []
with open("hist.csv", "r") as f:
    for line in f.readlines():
        _b, _c = [float(i) for i in line.split(",")]
        bins.append(_b)
        count.append(_c)

커브 피팅 함수

scipy.optimize.curve_fit() 함수는 직접 만든 모델의 최적 계수를 찾아줍니다. 이를 이용해서 피팅을 수행하고 계수를 찾아 적분에 필요한 정보를 얻습니다. 판단에 따라 다양한 모델 중 하나를 구현해서 사용할 수 있습니다. 여기서는 일반적으로 사용하는 가우시안(정규분포) 모델을 사용하도록 하겠습니다.

\[a_0 \exp\left(\frac{-(x- a_1 )^2}{2 a_2^2}\right) + a_3 \exp\left(\frac{-(x- a_4 )^2}{2 a_5^2}\right)\]

사용할 가우시안의 선형결합입니다.

1
2
3
4
5
6
7
8
9
10

def particle(x, a, b, c):
    return a * np.exp(-((x - b) ** 2) / (2 * c ** 2))


def model(x, a_0, a_1, a_2, a_3, a_4, a_5):
    p_a = particle(x, a_0, a_1, a_2)
    p_b = particle(x, a_3, a_4, a_5)
    return p_a + p_b

popt, pcov = curve_fit(model, bins, count, p0=[100, 1, 0.1, 100, 4, 0.1])

p0 옵션은 나중에 선형 결합된 상태로 피팅한 결과를 다시 각 입자의 에너지 스펙트럼으로 변환하는 과정에서 무엇이 입자 A, 입자 B의 결과인지 알기 쉽게 하기 위해 초기 변수를 지정하는 것입니다. 0번과 3번 값은 함수값의 최대치와 관련이 있고, 1번과 4번은 가우시안의 중앙이 어디에 있는지, 2번과 5번은 분산과 관련이 있습니다.

1번과 4번 초기값을 미리 주는 방법으로 어떤 입자의 에너지 스펙트럼인지 알기 쉽도록 만들었습니다.

popt는 최적값의 배열, popv는 공분산 배열입니다. 직접 출력해서 확인해 볼 수 있습니다. 공분산 popv로부터 표준 편차를 계산하려면 np.sqrt(np.diag(pcov))를 사용합니다.

1
2
3
4
5
6
7

xdata = np.linspace(0, 4, 100)

plt.plot(xdata, model(xdata, *popt), "k")
plt.plot(xdata, particle(xdata, *popt[:3]), "r")
plt.plot(xdata, particle(xdata, *popt[3:]), "b")
plt.bar(bins, count, 0.05, color="#AAA")
plt.show()

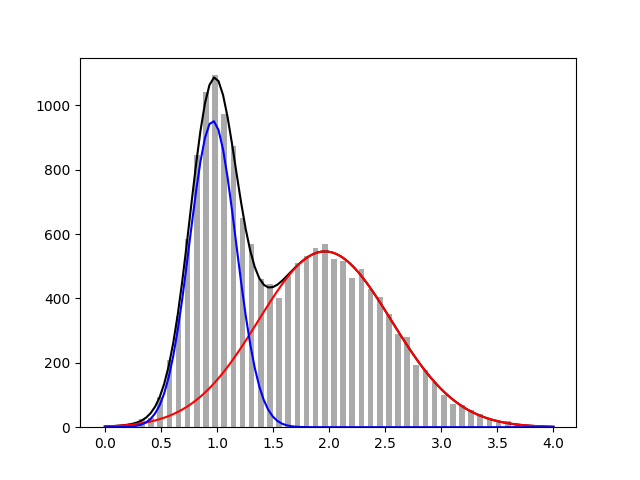
데이터 적분 2

피팅 결과를 눈으로 확인해봅시다. 우리가 세운 모델을 사용하여 두 입자의 스펙트럼을 분리할 수 있는 것을 볼 수 있습니다. 분리한 입자별 에너지 스펙트럼을 통해 다양한 정보를 얻을 수 있습니다.

xdata는 내삽을 적용하여 더욱 정밀한 값을 얻기 위해 np.linspace()함수를 사용했습니다.

적분 연산

앞서 두 입자의 생성비를 계산하기 위해 앞서 구한 모델로부터 두 입자의 함수를 구했습니다. 이제 각각의 에너지 스펙트럼을 적분하여 몇 개의 입자가 생성되었는지 비교하는 작업이 남았습니다.

적분을 통해 입자의 생성비를 계산할 수 있습니다. 여기서는 이전 시간에 검증한 scipy.integrate.trapezoid() 함수를 사용합니다.

1
2
3
4
5
6
7

p_a_value = trapezoid(particle(xdata, *popt[:3]), xdata)
p_b_value = trapezoid(particle(xdata, *popt[3:]), xdata)

print(f"Particle A: {p_a_value:.2f}")
print(f"Particle B: {p_b_value:.2f}")
print(f"Proportion particle data (A/B): {p_a_value/p_b_value:.3f}")
print(f"Proportion particle reference (A/B): {6000/10000:.3f}")

마지막 줄은 예제로 사용했던 데이터를 생성할때 정한 비율입니다.